Нормальное распределение.

Говорят, что случайная величина 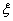нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения 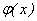имеет вид

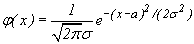
(28)

где a - любое действительное число, а 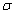> 0. Смысл параметров a и 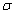будет установлен в дальнейшем (см. §4, п. 2). Исходя из связи между плотностью распределения 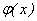и функцией распределения F(x) [см. формулу (22)], имеем

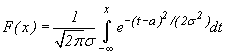
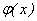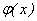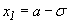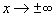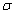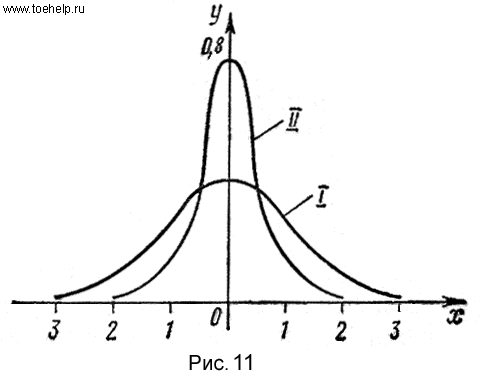
График функции симметричен относительно прямой x=a. Несложные исследования показывают, что функция достигает максимума при x=a, а ее график имеет точки перегиба при и . При график функции асимптотически приближается к оси Ox. Можно показать, что при увеличении кривая плотности распределения становится более пологой. Наоборот, при уменьшении 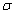график плотности распределения сжимается к оси симметрии. При a=0 осью симметрии является ось Oy. На рис. 11 изображены два графика функции y= 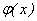. График I соответствует значениям a=0, 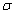=1, а график II - значениям a=0, 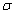=1/2.

Покажем, что функция 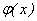удовлетворяе условию (24), т.е. при любых a и 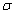выполняется соотношение

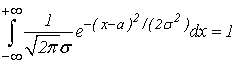
В самом деле, сделаем в этом интеграле замену переменной, полагая 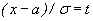. Тогда

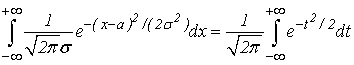
В силу четности подинтегральной функции имеем

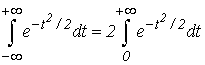
Следовательно,

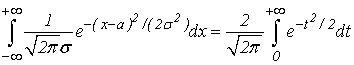
Но,

В результате получим

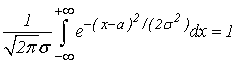
(29)

Найдем вероятность 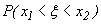. По формуле (23) имеем

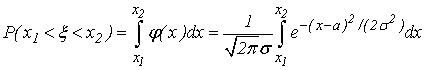
Сделаем в этом интеграле замену переменной, снова полагая 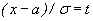. Тогда 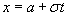, 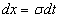и

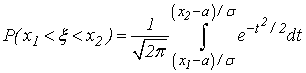
(30)

Как мы знаем, интеграл 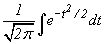не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (30) вводится функция

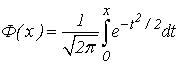
(31)

называемая интегралом вероятностей. Для этой функции составлены таблицы ее значений для различных значений аргумента (см. табл. II Приложения). Используя формулу (31) получим

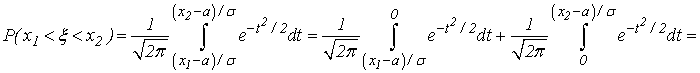
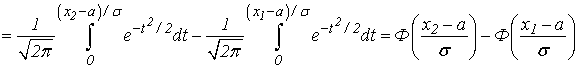
Итак,

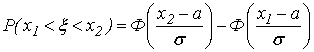
(32)

Легко показать, что функция Ф(х) (интеграл вероятностей) обладает следующими свойствами.
1°. Ф(0)=0
2°. 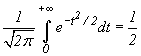; при 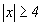величина 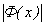практически равна 1/2 (см. табл. II).
3°. Ф(-x)=-Ф(х), т.е. интеграл вероятностей является нечетной функцией.

График функции Ф(х) изображен на рис. 12.

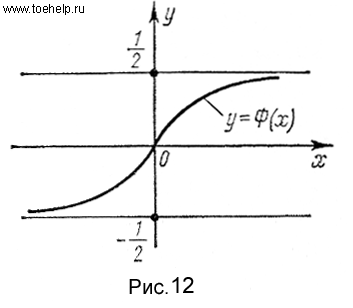
Таким образом, если случайная величина 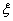нормально распределена с параметрами a и 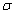, то вероятность того, что случайная величина удовлетворяет неравенствам 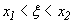, определяется соотношением (32).
Пусть 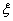> 0. Найдем вероятность того, что нормально распределенная случайная величина 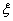отклонится от параметра a по абсолютной величине не более, чем на 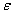, т.е. .
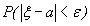Так как неравенство равносильно неравенствам 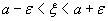, то полагая в соотношении (32) 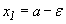, 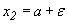получим

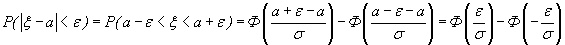
Вследствие того, что интеграл вероятностей - нечетная функция, имеем
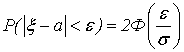