Примеры решения задач. Краткие теоретические сведения и основные формулы

Краткие теоретические сведения и основные формулы

Теория относительности – фундаментальная теория, устанавливающая пространственно–временные закономерности для любых физических процессов.

При учёте гравитационных полей теория относительности называется общей. Если влиянием гравитационных полей можно пренебречь, то теория относительности называется частной, или специальной.

Основой теории относительности являются два постулата, сформулированные А. Эйнштейном.

Первый постулат – принцип относительности: все физические явления в любых ИСО при одинаковых начальных условиях протекают одинаково. Принцип относительности Эйнштейна является обобщением механического принципа относительности на все явления физики.

Второй постулат – принцип инвариантности скорости света в вакууме: скорость света в вакууме не зависит от скорости движения источника света и наблюдателя и одинакова во всех инерциальных системах отсчёта (c = 3 ^.10⁸ 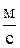= сonst).

В соответствии с двумя постулатами специальной теории относительности между координатами и временем в двух ИСО и существуют соотношения, которые называются преобразованиями Лоренца.

В случае, когда система движется относительно системы 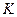вдоль оси OX (рис. 6.1) со скоростью 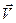, преобразования Лоренца для координат и времени имеют вид:

;

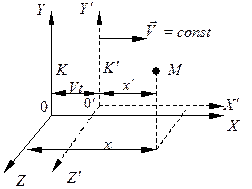
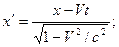
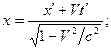
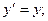
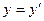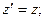
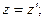
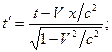
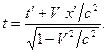
Рис.6.1

Из преобразований Лоренца следует вывод: не только пространственные координаты зависят от времени (как в преобразовании Галилея), но и время в обоих системах отсчёта зависит от пространственных координат, а также от скорости V движения системы отсчёта относительно .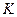

При условии V< < c преобразования Лоренца переходят в преобразования координат Галилея:

;

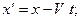
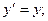
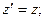
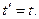
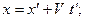
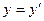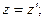
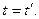
Принцип относительности Эйнштейна может быть сформулирован с учётом преобразований Лоренца следующим образом: все законы физики, описывающие любые физические явления, должны во всех ИСО иметь одинаковый вид. Это означает, что при переходе от одной ИСО 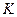к другой - с помощью преобразований Лоренца законы физики должны сохранять свою форму.

Закон сложения скоростей: если материальная точка М (рис.6.2) движется вдоль оси 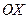, а следовательно, и 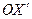в инерциальных системах 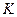и и имеет в этих системах отсчёта скорости, равные соответственно u и 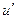, то

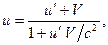
где V – скорость движения системы 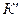относительно .

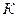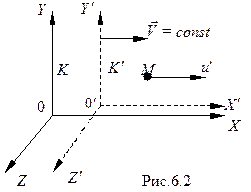
При 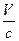< < 1 и 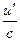< < 1 релятивистский закон сложения скоростей переходит в закон сложения скоростей в классической механике:

.

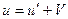Длина тела в различных ИСО. Длина тела в системе 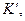где оно покоится, называется собственной длиной. Из преобразований Лоренца следует, что длина тела (масштаб) меняется при переходе от одной ИСО к другой и определяется соотношением:

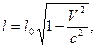
где 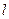- длина тела в ИСО, относительно которой тело движется; 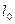- длина тела в ИСО, относительно которой оно покоится.

Сокращение длины – прямое следствие конечности скорости света. При V < < c лоренцовым сокращением можно пренебречь ().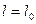

Длительность событий также относительна. Промежуток времени D t, измеренный в системе отсчёта, относительно которой тело неподвижно, называется собственным временем. Собственное время отсчитывается по часам, движущимся вместе с системой отсчёта. Из преобразований Лоренца следует, что

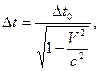
где D t – лабораторное время – промежуток времени, измеренный в ИСО, относительно которой тело движется.

Это означает, что часы, движущиеся относительно инерциальной системы отсчёта, идут медленнее неподвижных часов и показывают меньший промежуток времени между событиями (релятивистское замедление времени).

Закон взаимосвязи массы и энергии выражается формулой А. Эйнштейна:

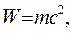
где 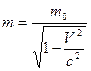- релятивистская масса частицы, она зависит от скорости V, с которой частица движется в данной системе отсчёта.

Полная энергия частицы равна произведению её релятивистской массы на квадрат скорости света в вакууме.

При условии 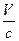< < 1 релятивистская масса принимает значение массы покоя, то есть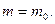

Наименьшая энергия 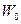частицы в системе, относительно которой она покоится (V = 0), называется собственной энергией, или энергией покоя:

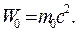
Полная энергия частицы равна сумме энергий движения (кинетической энергии 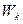и энергии покоя ):

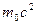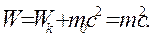
Между полной энергией 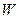и релятивистским импульсом P в специальной теории относительности существует связь

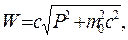
где 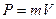- релятивистский импульс частицы, движущейся со скоростью V.

Импульс P и кинетическая энергия 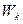связаны соотношением

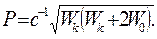
Примеры решения задач

Задача 1. При какой скорости движения тела релятивистское сокращение длины тела составляло бы: а) 1 %; б) 50 %?

Дано:

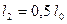
V ₁ -? V ₂ -?