Вычисления

Вычислим характеристики вращательного движения толстостенного цилиндра для момента времени t =0, 5 c.

Подставляя в формулу (1) числовые значения, получаем момент инерции тела

J = 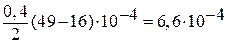(кг м²).

Угловая скорость в соответствии с формулой (3) равна

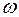=0, 2+ 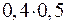=0, 40(рад/с).

Угловое ускорение вычислено в формуле (4).

Момент силы определяется по формуле (5)

М=6, 6 ·10^-4·0, 4=2, 64·10^-4(Н·м)

Момент импульса вычисляется в соответствии с выражением (6)

L= 6, 6 ·10^-4·0, 4=2, 64·10^-4(кг·м²/с).

Значение кинетической энергии определяется по формуле (7)

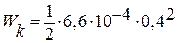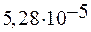= (Дж).

Работу внешней силы найдем по формуле (8)

А= 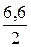·10^-4(0, 4²–0, 2²)=3, 96·10^-5Дж.

Мгновенная мощность рассчитывается по формуле (9)

N=0, 40·2, 64·10^-4=1, 06 Вт.

Линейная скорость равна (см. формулу (10))

(м /с).

Нормальное ускорение можно рассчитать, учитывая выражение (12),

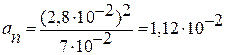(м/с²).

Тангенциальное ускорение определяется из соотношения (11)

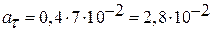(м/с²).

Полное ускорение можно вычислить из формулы (14)

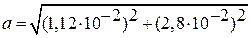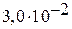= (м/с²).

Линейная скорость точки, расположенной на боковой поверхности, направлена по касательной к траектории – окружности (рис.1). Тангенциальное ускорение сонаправлено с линейной скоростью, а нормальное ускорение направлено по радиусу к центру окружности, через которую проходит ось вращения. Полное ускорение направлено по диагонали прямоугольника, построенного на нормальном и тангенциальном ускорениях как на сторонах.

Момент силы сонаправлен с угловым ускорением, а момент импульса совпадает по направлению с угловой скоростью (рис.2).Векторы, направления которых связаны с направлением вращения тела, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения и могут откладываться от любой точки оси вращения.

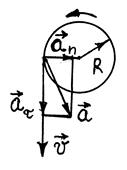
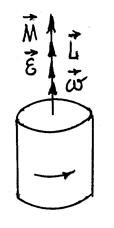
Рис. 1 Рис.2