Пример решения 2-ой ГПЗ.

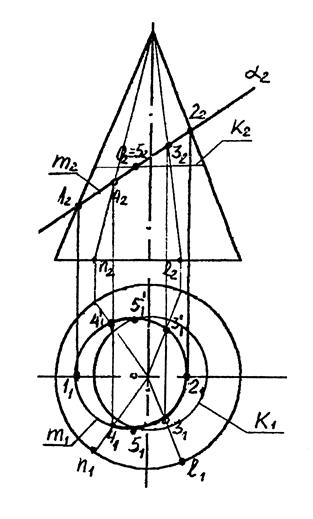
Рис. 5.

Определить проекции линии пересечения двух поверхносте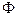й и 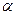. Учитывая соби­рательное свойство проекции 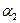плоскости 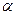, следует считать, что 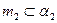, т.е. 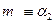(в пределах поверхности Ф). Вторая проекция линии пересечения m₁определяется по принад­лежности к поверхности конуса Ф. Любая точка, принадлежащая боковой поверхности конуса, может быть определена либо образующей конуса, либо с помощью параллелей. Опреде­ление точек 3₁ и 4₁ выполнено с помощью образующих 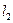и 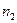, проведенных через произ­вольно взятые на линии 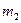точки 3₂ и 4₂. На горизонтальных проекциях 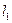и 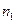определены точки 3₁ и 4₁ с помощью линии связи. Точка 5₂ взята в середине отрезка 1₂2₂, она будет совпадать с точкой пересече­ния осей эллипса (центром эллипса). Го­ризонтальная проекция точки 5 строится с помощью параллели К. Проекция 5₁ получится на пересечении линии связи и горизонтальной проекции параллели К₁.

Поскольку поверхность конуса Ф и плоскость α имеют общую плоскость симметрии (главную меридиональную плоскость), фигура сечения и ее горизон­тальная проекция симметричны относи­тельно этой плоскости. Поэтому точка во фронтальной проекции является двойной точкой, и ей соответствуют две точки в горизонтальной проекции.

Фигурой сечения в горизонталь­ной проекции является эллипс т₁, у ко­торой отрезок 1₁2₁ - большая ось, а отре­зок 5₁5₁’ - малая ось..

Можно сформулировать алгоритм решения ГПЗ для 2-ого случая.

1) Одна проекция искомого общего эле­мента уже непосредственно задана на чертеже;

2) Она принадлежит основной проекции проецирующего образа;

3) Вторую проекцию следует находить по принадлежности искомого общего элемента к не проецирующему образу

4. Решение ГПЗ в третьем случае расположения ГО относительно плоскостей

проекций

В этом случае ни одна из проекций искомого общего элемента не дана, т.к. нет про­ецирующих ГО, нет основных проекций..

Основным способом решения задач третьего случая является способ вспомогательных секущих поверхностей.

В качестве поверхностей посредников следует брать проецирующие поверхности. Решение ГПЗ третьего случая сводится к решению 2 ГПЗ второго случая, когда поверхности Δ - проецирующие, а заданные поверхности (Ф, 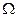) - не проецирующие. Целесообразно, в качестве таких проецирующих поверхностей брать проецирующие плоскости.

Проецирующие поверхности Δ желательно выбирать так, чтобы проекции линии были бы графически простыми линиями - прямыми или окружностями, что может быть не всегда возможным.

Пример решения l-й ГПЗ:

Имеются линия АВ и поверхность α.. Построить точку пересечения К, α; АВ [ .

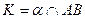1. Строим поверхность Δ, которой принадлежит АВ

[

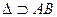
2. Строим линию пересечения поверхностей а и Δ

[

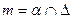
3. Строим точку пересечения К, которая находится на пересечении т и АВ

[

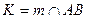
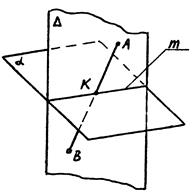
Рис. 6.

Пример решения 2-й ГПЗ

Имеются две поверхности Ф и .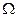

Построить линию пересечения поверхностей: [ .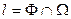

1. Строим проецирующую поверхность Δ ¹, которая пересекает заданные Ф и 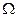: [Δ ¹ .

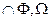2. Линией пересечения Δ ¹ с поверхностью Ф является линия т, [ 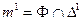и также п – с поверхностью .

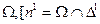3. На пересечении линий т и п находится точка К - общая для поверхностей Ф и :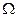

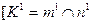
Затем решение повторяется для поверхности Δ ² и Δ ³ и т.д.

4.

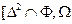
5.

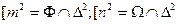
6.

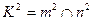
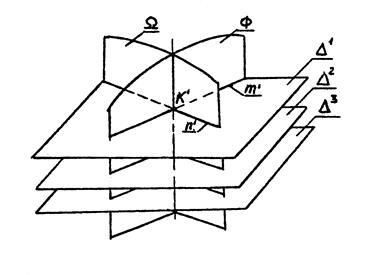
Рис. 7.

Строим линию пересечения L поверхностей Ф и :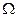

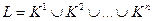
Сравнивая алгоритмы решения 1 ГПЗ и 2 ГПЗ в третьем случае, очевидно, что они, в принци­пе, одинаковы. Лишь последняя позиция алгоритма 2 ГПЗ не укладывается в алгоритме 1 ГПЗ, т.к. об­щим элементом двух пересекающихся ГО в 1 ГПЗ является точка, во 2 ГПЗ - линия.