Способ вспомогательных секущих сфер

Рассмотрим две основные поверхности вращения, т.е. две поверхности вращения с общей осью j. Меридианами заданных поверхно­стей являются образующая сферы u и образующая конуса 1, лежащие в одной плоскости. Эти мери­дианы будут пересекаться. Образующие 1 и u пере­секаются в точках 1 и 2. При вращении образую­щих 1 и u точки 1 и 2 перемещаются по окружно­стям т₁ и m₂. Эти окружности будут принадлежать общим поверхностям, а потому являются их ли­ниями пересечения.

Можно сделать вывод, что соосные поверх­ности пересекаются по окружностям - параллелям, число которых определяется числом точек пересечения их меридианов.

Если сфера будет соосной с любой поверх­ностью вращения, пересечет ее по окружностям ­параллелям, то ее можно использовать в качестве поверхности -посредника.

Если центр сферы поместить в точку пере­сечения осей поверхностей вращения, то такая сфера будет пересекать обе поверхности по окружностям, которые будут являться линиями пе­ресечения сферы с каждой из заданных поверхно­стей.

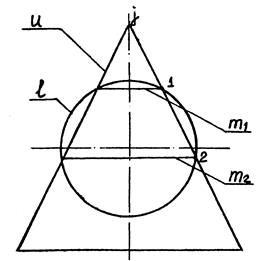
Рис. 10.

Пример решения 2-й ГПЗ. Способ вспо­могательных секущих сфер.

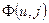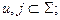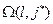
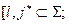
[ u 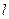φ j ]

φ j]

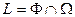
Алгоритм решения:

1.1.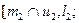

1.2. 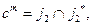где 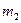- очерк сферы на π _2.

2.1.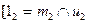

2.2.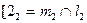

2.3.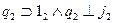

2.4.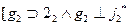

2.5.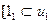

2.6.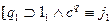

3.1.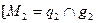

3.2. ­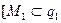

4.1.

4.2.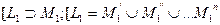

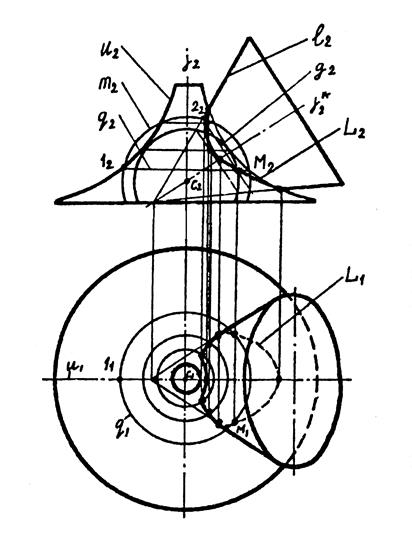
Рис. 11.

Секущие сферы имеют пределы.

Сфера, вписанная в большую из поверхностей Ф и 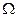, является минимальной. В на­шем случае такой сферой будет сфера, вписанная в Ф. Она пересекает 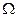по окружности 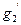и касается Ф по окружности 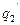. Сферы меньшего радиуса не будут иметь общих точек с по­верхностью Ф и потому не могут быть использованы в роли секущих поверхностей-­посредников.

Самая большая сфера - это та, которую есть смысл проводить через наиболее удален­ную от центра точку линии пересечения. Такой точкой является точка пересечения проекций очерковых образующих поверхностей Ф и 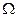. В указанной точке окружности g и q касаются друг друга, представляя собой предельный случай пересечения g и q.

Рассмотренный способ построения линии пересечения называют способом концен­трических сфер.