
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение прямоугольной изометрической проекции
|
|
В изометрии аксонометрические оси расположены под углом 120 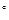 по отношению друг к другу (Рис. 12 б).
по отношению друг к другу (Рис. 12 б).
Коэффициенты искажения линейных размеров вдоль изометрических осей равны u = v = w = 0, 82. Это - истинные коэффициенты искажения. Следовательно, при переходе от комплексного чертежа к изометрической проекции все линейные размеры отрезков прямых, параллельных осям координат, сокращаются до 0, 82 их натуральной величины. Для устранения линейной арифметической операции - умножения длин указанных отрезков на 0, 82 введены приведенные коэффициенты искажения:
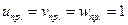
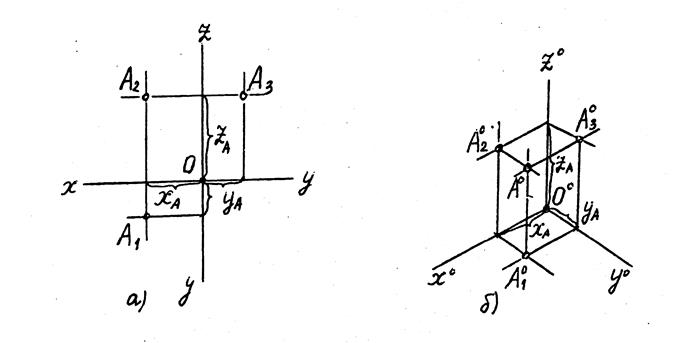
Рис. 12.
В результате при построении изометрии с использованием приведенных коэффициентов искажения линейные размеры вдоль осей ОХ, OУ и OZ комплексного чертежа переносятся параллельно изометрическим осям O0X0, O0Y0 и O0Z0 в натуральную величину.
Рассмотрим построение изометрической проекции точки А (Рис. 12, б).
Имеем комплексный чертеж точки А: А1 (XA, YA), A2 (XA, ZA), A3 (YA, ZA) (Рис.12 а). Откладываем отрезки ХА, УА, ZA на координатных изометрических осях O0X0, O0Y0 и O0Z0 без искажения (Рис.12 б). Вторичную проекцию А10 получаем на пересечении прямых, проведенных из концов отрезков ХА параллельно оси O0Y0 и УА параллельно оси O0X0. Из точки А10 проводим прямую, параллельную оси O0Z0, откладываем на ней координату ZA и получаем главную изометрическую проекцию точки А – А0. Аналогично можно построить вторичные проекции А20 по координатам ХА, ZА и А30 по координатам УА, ZА, а затем и главную изометрическую проекцию точки А – А0.
При построении изометрической проекции Δ АВС строим аксонометрические проекции точек, A0, B0 и C0, а затем соединяем их прямыми линиями.
Лист 2
Задание: Построить натуральный вид сечения плоскостью данного тела и полную развертку поверхности усеченной его части.
Таким образом, задача разбивается на три части: сначала надо построить сечение в плоскостях П 1и П 2, затем определить его натуральную величину. После чего строить развертку оставшейся части.
Найдем все точки пересечения фронтально-проецирующей плоскости S с ребрами пирамиды и соединим их отрезками прямой. Фронтальная проекция S2 пересекает ребра пирамиды в точках А2, В2, С2, Д2, Е2, F2. По линиям связи находим их горизонтальные проекции А1, В1, С1, Д1, Е1, F1 на горизонтальных проекциях соответствующих ребер. Соединяя найденные точки, получаем линию пересечения А1В1С1Д1Е1F1 заданной плоскости с пирамидой. Плоская фигура, ограниченная полученной линией, и является сечением пирамиды плоскостью. В нашем примере это шестиугольник АВСДЕF.
Для определения натуральной величины шестиугольника АВСДЕF способом замены плоскостей проекций вводим вместо П1 плоскость П5, параллельную плоскости шестиугольник АВСДЕF. Тогда получается система плоскостей проекций П2/П5, ось Х 25 которой параллельна А2В2С2Д2Е2F2. Она может быть расположена на произвольном расстоянии от А2В2С2Д2Е2F2. Далее из точек А2, В2, С2, Д2, Е2, F2 проводим линии связи перпендикулярно Х 25, и на каждой из них от оси Х 25 откладываем отрезок, равный расстоянию от горизонтальной проекции соответствующей точки до оси Х 12. Затем отложим на построенных перпендикулярах отрезки, равные расстояниям от оси П 2/ П 1, которую считаем расположенной на основании пирамиды, до соответствующих проекций А1, В1, С1, Д1, Е1, F1. Соединив указанные точки, получим натуральную величину сечения пирамиды заданной плоскостью S.
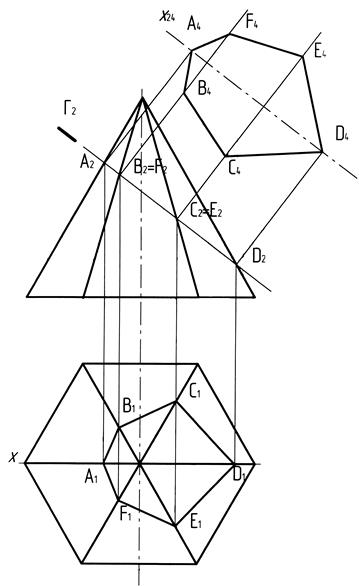
Рис. 13