Применение нормального распределения

Как уже упоминалось, при обследованиях выборки часто достаточно велики, так что получаемые по ним оценки имеют приблизительно нормальное распределение. Для вероятностного отбора, кроме того, существуют формулы среднего значения и дисперсии оценки. Рассмот-рим сначала несмещенные оценки. Оценка 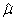, получаемая согласно некоторой схеме отбора, называется несмещенной оценкой некоторой характеристики совокупности, 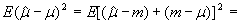, если среднее значение* 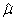, взятое по всем возможным выборкам, равно 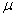. В обозначениях параграфа 1.5 это условие можно записать в виде

,

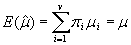где 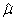- оценка, получаемая по i -й выборке. Символ Е, заменяющий выражение < математическое ожидание величины> (the expected value of), общепринят.

Предположим, что мы получили выборку методом, обеспечивающим несмещенную оценку, и вычислили соответствующее значение выборочной оценки 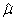и ее среднее квадратичное отклонение 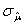(часто называемое иначе ее стандартной ошибкой**). Насколько хороша наша оценка? Мы не знаем точную величину ошибки оценки ( 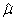- 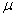), но из свойств нормального распределения вытекает, что с вероятностями:

0, 32 (или приблизительно в одном случае из трех) абсолютное значение ошибки | 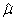- 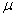| превосходит ;

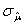0, 05 (или в одном случае из двадцати) абсолютное значение ошибки | 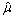- 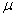| превосходит 1, 96 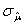> 2 ;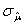

0, 01 (или в одном случае из ста) абсолютное значение ошибки | 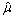- 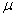| превосходит 2, 58 .

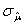Например, если при определении срока службы некоторых приборов на большом предприятии при обычной нагрузке вероятностная [[26]] выборка показала, что среднее время работы прибора для этой выборки 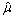= 394 дням при среднем квадратичном отклонении (стандартной ошибке) 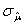= 4, 6 дня, то среднее время работы приборов для всей их совокупности в 99 случаях из ста заключено между

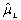= 394 - (2, 58) (4, 6) = 382 дням

и

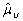= 394 + (2, 58) (4, 6) = 406 дням.

Эти границы, 382 дня и 406 дней, называются нижней (lower) и верхней (upper) доверительными границами. Для отдельной оценки, сделанной по однократному обследованию, утверждение < и, заключено между 382 и 406 днями> не является абсолютно правильным. < 99%-ный доверительный уровень> означает, что если бы та же схема отбора мно-гократно применялась к рассматриваемой совокупности и утверждение о доверительных границах делалось по каждой выборке, то приблизи-тельно в 99% случаев оно было бы правильным и в 1 % случаев ошибоч-ным. Если выборочный метод применяется там, где ранее производи-лись сплошные переписи, то это свойство иногда можно продемонст-рировать, извлекая повторно выборки предлагаемого типа из совокуп-ности, по которой имеются полные данные, так что р. известно [см., на-пример, (Trueblood and Cyert, 1957)]. Практические работники лучше и глубже понимают природу выборочного метода, убедившись на деле в том, что за небольшим исключением заранее установленная доля утверждений оказывается правильной. Подобным же образом, если извлекается однократная выборка из каждой совокупности, принад-лежащей некоторому ряду различных совокупностей, то окажутся правильными приблизительно 95% утверждений, сделанных на 95%-ном доверительном уровне.

Ранее предполагалось, что 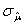, вычисленное по выборке, определяется точно. В действительности 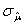, как и 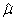, подвержено ошибкам выборки. Если случайная переменная распределена нормально, то при малом объеме выборки для нахождения доверительных границ для 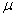вместо таблиц нормального распределения применяются таблицы t? распределения Стьюдента. Замена таблиц нормального распределения таблицами t? распределения почти не играет роли, если число степеней свободы при вычислении 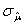превосходит 60. При некоторых видах расслоенного отбора и применении метода дублированного отбора (см. параграф 13.14) число степеней свободы невелико и необходимо пользоваться таблицами t? распределения.