
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция распределения вероятностей
|
|
двумерной случайной величины и её свойства
Универсальной формой задания двумерной случайной величины является функция распределения (или «интегральная функция»).
Функцией распределения двумерной случайной величины (X, Y) называют вероятность совместного выполнения двух неравенств {X< x} и {Y< y}:
 . (1)
. (1)
Геометрическая интерпретация: если двумерную случайную величину (X, Y) рассматривать как случайную точку в прямоугольной декартовой системе координат, то функция распределения F(x, y) есть вероятность попадания случайной точки (X, Y) в бесконечный квадрант с вершиной в точке (x, y), лежащий левее и ниже её (рис.3):

Рис. 3. Геометрическая интерпретация функции распределения
двумерной случайной величины
В аналогичной интерпретации функция распределения первой компоненты X случайного вектора – обозначим её F1(x) – представляет собой вероятность попадания случайной точки в полуплоскость, ограниченную справа абсциссой х (рис. 4); функция распределения величины Y – F2(y) – вероятность попадания в полуплоскость, ограниченную сверху ординатой y (рис. 5):
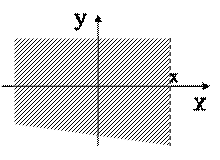
Рис. 4. Геометрическая интерпретация функции распределения первой компоненты F1(x) двумерной случайной величины (X, Y).

Рис. 5. Геометрическая интерпретация функции распределения второй компоненты F2(y) двумерной случайной величины (X, Y).
Пример 1. Найти вероятность того, что в результате испытания составляющая X двумерной случайной величины (X, Y) примет значение X< 2, при этом составляющая Y примет значение Y< 3, если известна функция распределения системы
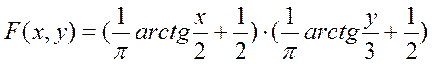
Решение: 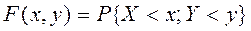
Тогда
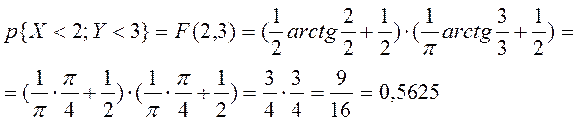
Ответ: 0, 5625.