
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства функции распределения двумерной случайной величины
|
|
1) 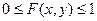 , (2)
, (2)
так как это вероятность.
2) F(x, y) есть неубывающая функция своих аргументов, то есть
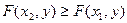 при
при 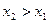 , (3)
, (3)
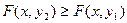 при
при 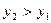 . (4)
. (4)
Доказательство. При увеличении какого-либо из аргументов (x, y) заштрихованная на рис.1 область увеличивается, значит, вероятность попадания в неё случайноё точки (X, Y) не может уменьшаться.
3) Если хотя бы один из аргументов обращается в -∞, то функция распределения F(x, y) равна нулю:
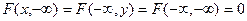 . (5)
. (5)
Доказательство. События  и их произведение невозможны, следовательно, вероятности этих событий равны нулю.
и их произведение невозможны, следовательно, вероятности этих событий равны нулю.
4) Если оба аргумента равны +∞, то функция распределения F(x, y) равна единице:
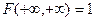 . (6)
. (6)
Доказательство. Событие 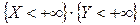 достоверно, следовательно, его вероятность равна единице.
достоверно, следовательно, его вероятность равна единице.
5) При одном из аргументов, равном +∞, функция распределения двумерного вектора превращается в функцию распределения компоненты, соответствующей другому аргументу:
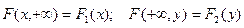 . (7)
. (7)
Доказательство: Так как событие Y< +∞ достоверно, то F(x, +∞) определяет вероятность события X < x, то есть представляет собой функцию распределения составляющей X.
Итак, зная совместное распределение двух случайных величин, можно найти одномерные распределения каждой из этих случайных величин, однако обратное, в общем случае, неверно.
Вероятность попадания случайной точки в полуполосу
 Используя функцию распределения системы случайных величин Х и Y, найдем вероятность того, что в результате испытания случайная точка попадет в полуполосу x1< X< x2 и Y< y
Используя функцию распределения системы случайных величин Х и Y, найдем вероятность того, что в результате испытания случайная точка попадет в полуполосу x1< X< x2 и Y< y
 y (x1, y) (x2, y)
y (x1, y) (x2, y)
p{x1< X< x2, Y< y} = 
= p(x< x2, Y< y) - p{ X< x1, Y< y}= 







= F(x2, y) - F(x1, y)
x1 x2 x
Аналогично, y










 p{X< x, y1< Y< y2} = F(x, y2) - F(x, y1). y2 (x, y2)
p{X< x, y1< Y< y2} = F(x, y2) - F(x, y1). y2 (x, y2)
 Таким образом, вероятность попадания случайной
Таким образом, вероятность попадания случайной

 точки в полуполосу равна приращению функции (x, y1)
точки в полуполосу равна приращению функции (x, y1)
 распределения по одному из аргументов. y1
распределения по одному из аргументов. y1
 x x
x x