Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дискретной двумерной случайной величины
|
|
Законом распределения вероятностей дискретной двумерной случайной величины называется совокупность всех возможных значений этой случайной величины, то есть пар чисел (xi, yi), и их вероятностей p(xi, yi):
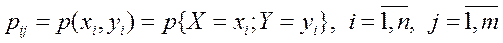
Здесь n, m – число возможных значений случайных величин X и Y (n и m могут быть конечными или бесконечными).
Обычно закон распределения задают в виде таблицы. Пусть x1, x2, …, xn – все возможные значения случайной величины X, y1, y2, …, ym – все возможные значения случайной величины Y. Тогда закон распределения может быть представлен в виде следующей таблицы:
Таблица 1
 y
x
| y1 | y2 | … | yj | … | ym |
| x1 | p(x1, y1) | p(x1, y2) | … | p(x1, yj) | … | P(x1, ym) |
| x2 | p(x2, y1) | p(x2, y2) | … | … | … | … |
| … | … | … | … | … | … | … |
| xi | p(xi, y1) | … | … | p(xi, yj) | … | … |
| … | … | … | … | … | … | … |
| xn | p(xn, y1) | … | … | … | … | p(xn, ym) |
В клетке на пересечении строки xi и столбца yj указана вероятность p(xi, yj) того, что двумерная случайная величина (X, Y) примет значение (xi, yj).
Так как события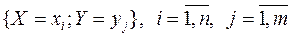 
образуют полную группу событий, то сумма вероятностей во всех клетках равна единице:
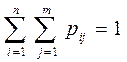(9)
Зная закон распределения двумерной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, так как, например, события {X=x1, Y=y1}, {X=x1, Y=y2}, …, {X=x1, Y=ym} несовместны, то вероятность p(x1) того, что одномерная случайная величина X примет значение x1, по теореме сложения вероятностей несовместных событий равна
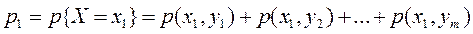. (10)
В общем случае имеем:
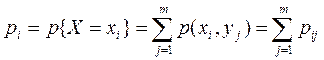. (11)
Аналогично можно записать:
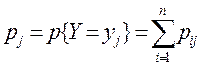. (12)
Пример 3. Качество продукции характеризуется двумя случайными величинами: X и Y. Закон распределения случайного вектора (X, Y) представлен в таблице:
Таблица 2
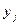
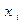
| 0, 1 | 0, 2 | 0, 3 |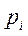 
| |
| 0, 2 | 0, 1 | 0, 05 | 0, 05 | 0, 4 | |
| 0, 15 | 0, 15 | 0, 1 | 0, 4 | ||
| 0, 1 | 0, 1 | 0, 2 | |||
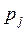
| 0, 2 | 0, 25 | 0, 3 | 0, 25 |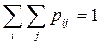 
|
Найдём закон распределения координат X и Y случайного вектора. Вероятность события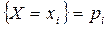 
есть сумма вероятностей, находящихся в i-ой строке. Вероятности 
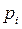находятся в последнем столбце таблицы.
Ряд распределения случайной величины Х имеет вид:
Таблица 3
| |||
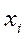
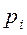
| 0, 4 | 0, 4 | 0, 2 |
Ряд распределения Y находим, вычисляя суммы элементов столбцов таблицы 2. Эти вероятности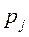 
находятся в последней строке таблицы 2.
Ряд распределения случайной величины Y имеет вид:
Таблица 4
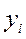
| 0, 1 | 0, 2 | 0, 3 | |
|
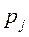
| 0, 2 | 0, 25 | 0, 3 | 0, 25 |