
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение регрессии в матричной форме можно записать в следующем виде
|
|
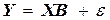 (8)
(8)
где введены следующие матрицы:
1) матрица-столбец (вектор) значений отклика в i- х точках эксперимента 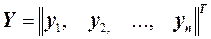 . Здесь индекс «Т» означает операцию транспонирования матрицы – перевод столбца в строку матрицы;
. Здесь индекс «Т» означает операцию транспонирования матрицы – перевод столбца в строку матрицы;
2) матрица планирования эксперимента, которая задает координаты всех опытных точек 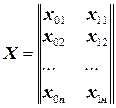 ,
,
где введена фиктивная переменная 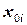 , тождественно равная единице при всех значениях плана;
, тождественно равная единице при всех значениях плана;
3) матрица-столбец (вектор) искомых коэффициентов регрессии
 .
.
Здесь 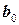 постоянная регрессии, которая в уравнении (2) обозначена через а;
постоянная регрессии, которая в уравнении (2) обозначена через а;
4) матрица-строка (вектор) флюктуаций или помех
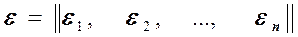 .
.
С учетом матричных обозначений сумму квадратов остатков можно представить в виде
 . (9)
. (9)
Дифференцируя 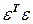 по В и приравнивая полученную производную нулю, получим систему нормальных уравнений в матричной форме:
по В и приравнивая полученную производную нулю, получим систему нормальных уравнений в матричной форме:
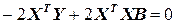
или  . (10)
. (10)
Матричная форма нормальных уравнений (10) для линейного уравнения регрессии равносильна системе алгебраических уравнений:

В уравнении (10) матрица 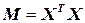 называется информационной матрицей, или матрицей системы нормальных уравнений.
называется информационной матрицей, или матрицей системы нормальных уравнений.
Матрица-столбец b - коэффициентов определяется из уравнения (10) путем умножения слева обеих его частей на матрицу 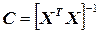 , которая называется дисперсионной, так как с ее помощью устанавливаются оценки дисперсий b - коэффициентов. В результате имеем
, которая называется дисперсионной, так как с ее помощью устанавливаются оценки дисперсий b - коэффициентов. В результате имеем
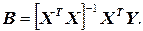 (11)
(11)
3. Решение задачи регрессионного анализа в случае ортогонального плана
Методика построения моделей на основе ортогональных планов состоит в переходе к кодированной переменной U, обладающей свойствами симметрии относительно нового начала координат, совпадающего со средним значением 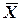 физической переменной X. Связь между физической переменной X и кодированной переменной U устанавливается с помощью уравнения кодирования
физической переменной X. Связь между физической переменной X и кодированной переменной U устанавливается с помощью уравнения кодирования
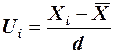 , (12)
, (12)
где d —шаг квантования переменной X.
При этом предполагается, что отклик Y измеряется при равноотстоящих значениях фактора X. Кодирование переменной по формуле (12) приводит к тому, что кодированная переменная принимает симметричные относительно нуля значения такие, что имеет место условие  .
.
Ортогональность плана приводит к диагональной информационной матрице
 . (13)
. (13)
Например, соответственно для пяти и семи опытных точек плана получим следующие информационные матрицы:
 ;
;

 .
.
Таким образом, в случае ортогонального плана информационная матрица является диагональной. Из нее легко получается обратная (дисперсионная) матрица
 . (14)
. (14)
Для пяти и семи опытных точек плана дисперсионные матрицы соответственно равны:
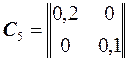 ;
;  .
.
В общем случае при ортогонализации и кодировании факторов значения элементов дисперсионной матрицы не зависит от реальных значений фактора X, а зависит только от числа опытных точек плана n.
Зная матрицу С, нетрудно найти b – коэффициенты. Так как для кодированных переменных ui
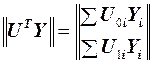 , (15)
, (15)
то из формулы (11) получим
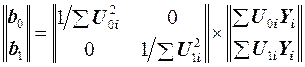 (16)
(16)
Отсюда находим выражения для b – коэффициентов:
 ;
; 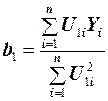 . (17)
. (17)
Пример 3. Для исходных данных, приведенных в табл. 5 определите параметры уравнения регрессии, приведя исходные данные к ортогональному плану.
Таблица 5
| Исходные данные | Расчет элементов определителей | |||||
| i | Xi | Yi | U0i | U1i | U0i Yi | U1i Yi |
| -2 | -12 | |||||
| -1 | -9 | |||||
| S |
Решение. Выполним необходимые расчеты (см. табл. 5) для решения уравнений (17). В результате получим:
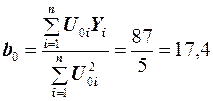 ;
; 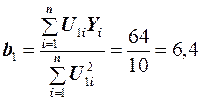 .
.
С учетом формулы (12) кодирования фактора 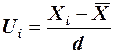 перейдем к физической переменной X и получим уравнение регрессии в том же виде, который ранее был найден без допущений об ортогональности плана
перейдем к физической переменной X и получим уравнение регрессии в том же виде, который ранее был найден без допущений об ортогональности плана
 .
.