Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальное распределение. Непрерывная СВ X имеет нормальное распределение, если ее плотность распределения имеет вид:
|
|
Непрерывная СВ X имеет нормальное распределение, если ее плотность распределения имеет вид:
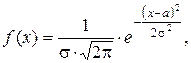 (1.47)
(1.47)
где a и s – параметры нормального распределения, s > 0.
Функция распределения нормально распределенной СВ X определяется формулой:
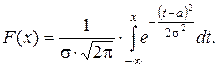 (1.48)
(1.48)
Числовые характеристики M (X) и D (X) соответственно равны:
M (X) = a, D (X) = s2.
Важную роль в теории играет центрированная и нормированная СВ X, для которой a = 0, s = 1. Иногда такое распределение СВ X называется стандартным. Плотность распределения нормальной стандартной СВ 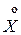 обозначается j(x), где
обозначается j(x), где
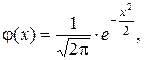 (1.49)
(1.49)
Функция распределения стандартной СВ X имеет вид:
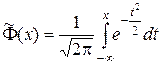 (1.50)
(1.50)
и называется функцией Лапласа.
Для удобства вычислений вводят функцию
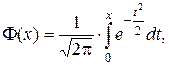 (1.51)
(1.51)
также называемую функцией Лапласа или нормированной функцией Лапласа.
Эти две функции связаны соотношениями:
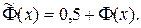 (1.52)
(1.52)
Функция Лапласа F(X) обладает свойствами:
1) Ф(0) = 0, 2) Ф(– x) = – Ф(x) (нечетная функция); 3) Ф(+¥) = 0, 5.
График плотности распределения вероятности нормально распределенной СВ X называется нормальной кривой или кривой Гаусса.
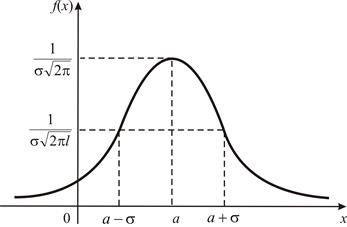
Рис. 3
Вероятность попадания значений СВ X, имеющей нормальное распределение с параметрами а и s, на участок (x 1; x 2)выражается формулой:
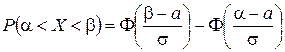 (1.53)
(1.53)
Если участок (a, b) симметричен относительно a, то вероятность попадания в него
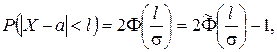 (1.54)
(1.54)
где 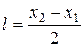 – половина длины участка.
– половина длины участка.
Нормальное распределение имеет исключительно важное значение в теории вероятностей.
Нормальному закону подчиняются, при определенных условиях, ошибки измерений, величины износа деталей в механизмах, ошибки стрельбы, величина шума в радиоприемном устройстве.
Главная особенность нормального закона распределения состоит в том, что он является предельным законом, к которому приближаются, при определенных условиях, другие законы распределения.
Например, при обработке деталей на станке-автомате, отклонение размеров деталей от номинального вызывается многими причинами. К ним относятся: колебание режима обработки, неточности установки и базировки деталей в приспособлении, износ режущего инструмента, неоднородность обрабатываемого материала, износ деталей станка и т. д. Каждая из этих причин влияет на размер деталей. Поэтому отклонение фактического размера детали от нормального можно представить как сумму большого числа отклонений, вызванных перечисленными выше причинами. Если слагаемые отклонения примерно одного порядка, то суммарное отклонение является случайной величиной, имеющей распределение, асимптотически приближающееся к нормальному.
Условия, при которых эти случайные величины 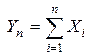 и
и 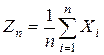 асимптотически нормальны, составляют содержание различных формулировок центральной предельной теоремы для одинаково распределенных и различно распределенных случайных величин.
асимптотически нормальны, составляют содержание различных формулировок центральной предельной теоремы для одинаково распределенных и различно распределенных случайных величин.
Теорема 1. Если случайные величины X 1, X 2, …, Xn независимы, одинаково распределены и имеют конечные M (Xi) = a и D (Xi) = s2 > 0, то
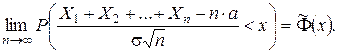
Теорема 2(Ляпунова). Если случайные величины X 1, X 2, …, Xn независимы и имеют конечные M (Xi) = ai, 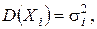
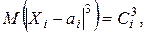 тогда
тогда
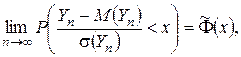
где 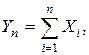

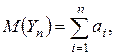
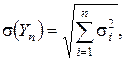
 если
если