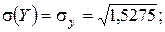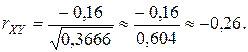Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции одного и двух дискретных случайных аргументов. Совместное распределение двух дискретных случайных величин
|
|
Пример 1. Заданы законы распределения двух независимых величин X и Y:
| xi | и | yi | |||||
| pi | 0, 3 | 0, 5 | 0, 2 | pi | 0, 6 | 0, 4 |
Найти законы распределения случайных величин Z = X – Y и W = XY.
Решение. Найдем возможные значения случайной величины Z. Для этого определим zij = xi – yj и расположим найденные значения в порядке возрастания:
z 11 = x 1 – y 1 = 0, z 12= 1 – 2= –1, z 21= 2 – 1= 1, z 22= 2 – 2= 0, z 31= 3 – 1= 2,
z 32= 3 – 2= 1, z 12= 1 – 2= –1, z 1= –1, z 2= 0, z 3= 1, z 4= 2.
Определим соответствующие им вероятности:
p 1 = P (Z = –1) = P (X = 1, Y = 2) = P ((X = 1) × (Y = 2)) =
= P (X = 1) × (Y = 2) = 0, 3 × 0, 4 = 0, 12;
p 2 = P (Z = 0) = P ((X = 1, Y = 1) + (X = 2, Y = 2)) =
= P (X = 1) × P (Y = 1) + P (X = 2) × P (Y = 2) = 0, 3 × 0, 6 + 0, 5× 0, 4 = 0, 38;
p 3 = P (Z = 1) = P ((X = 2, Y = 1) + (X = 3, Y = 2)) =
= P (X = 2) × P (Y = 1) + P (X = 3) × P (Y = 2) = 0, 5 × 0, 6 + 0, 2× 0, 4 = 0, 38;
p 4 = P (Z = 2) = P (X = 3, Y = 1) = P (X = 3) × P (Y = 1) = 0, 2 × 0, 6 = 0, 12.
При вычислении вероятностей pi используются правила вычисления вероятностей произведения независимых событий и суммы несовместных событий.
Ряд распределения СВ Z имеет вид:
| zi | –1 | |||
| pi | 0, 12 | 0, 38 | 0, 38 | 0, 12 |
Контроль: 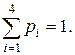
Аналогично находим ряд распределения случайной величины
W = X × Y.
Найдем wij = xiyj: w 11 = 1 × 1 = 1, w 12 = 1 × 2 = 2, w 21 = 2 × 1 = 2,
w 22 = 2 × 2 = 4, w 31 = 3 × 1 = 3, w 32 = 3 × 2 = 6.
Тогда w 1 = w 11 = 1, w 2 = w 21 = w 12 = 2, w 3 = w 31 = 3, w 4 = w 22 = 4,
w 5 = w 32 = 6.
p 1 = P (W = 1) = P (X = 1, Y = 1) = P (X = 1) × (Y = 1) = 0, 3 × 0, 6 = 0, 18;
p 2 = P (W = 2) = P ((X = 1, Y = 2) + (X = 2, Y = 1)) =
= P (X = 1) × P (Y = 2) + P (X = 2) × P (Y = 1) = 0, 3 × 0, 4 + 0, 5× 0, 6 = 0, 42;
p 3 = P (W = 3) = P (X = 3, Y = 1) = P (X = 3) × P (Y = 1) = 0, 2× 0, 6 = 0, 12;
p 4 = P (W = 4) = P (X = 2, Y = 2) = P (X = 2) × P (Y = 2) = 0, 5 × 0, 4 = 0, 20;
p 5 = P (W = 6) = P (X = 3, Y = 2) = P (X = 3) × P (Y = 2) = 0, 2 × 0, 4 = 0, 08.
Ряд распределения СВ W имеет вид:
| wi | |||||
| pi | 0, 18 | 0, 42 | 0, 12 | 0, 20 | 0, 08 |
Контроль: 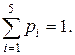
Пример 2. Задана таблица распределения двумерной случайной величины (X, Y):
| Y X | –1 | ||
| 0, 15 | 0, 2 | 0, 25 | |
| 0, 2 | 0, 1 | 0, 1 |
Определить: а) безусловные законы распределения СВ X и Y;
б) функцию распределения F (x; y) двумерной СВ (X; Y);
в) P (X ≤ Y);
г) условный закон распределения СВ Y при X = x 2 и M  ;
;
д) зависимость или независимость компонент X и Y;
е) центр рассеивания: точку (M (X); M (Y));
ж) закон распределения случайной величины Z = XY;
з) коэффициент корреляции rxy.
Решение. а) Суммируя вероятности в первой и второй строках таблицы, найдем вероятности возможных значений СВ X: x 1 = 1 и x 2 = 2.
P (X = x 1) = P (X = 1) = 0, 15 + 0, 2 + 0, 25 = 0, 6;
P (X = x 2) = P (X = 2) = 0, 2 + 0, 1 + 0, 1 = 0, 4.
Суммируя вероятности в каждом из столбцов таблицы, определим вероятности соответствующих значений СВ Y: y 1 = –1, y 2 = 1, y 3 = 2:
P (Y = y 1) = P (Y = –1) = 0, 15 + 0, 2 = 0, 35;
P (Y = y 2) = P (Y = 1) = 0, 2 + 0, 1 = 0, 3;
P (Y = y 3) = P (Y = 2) = 0, 25 + 0, 1 = 0, 35.
Законы распределения СВ X и Y имеют вид:
| xi | , | yi | –1 | . | ||||
| pi | 0, 6 | 0, 4 | pi | 0, 35 | 0, 3 | 0, 35 |
б) Функцию распределения заданной двумерной СВ (X; Y) найдем, используя формулу (1.60)
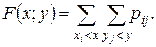
Если x ≤ 1 или y ≤ –1, то F (x; y) = 0 (события (X < x) или (Y < y) при этом являются невозможными).
Если 1 < x ≤ 2 и –1 < y ≤ 1, то F (x; y) = P (X = 1; Y = –1) = 0, 15.
Если 1 < x ≤ 2 и 1 < y ≤ 2, то F (x; y) = P (X = 1; Y = –1) + P (X = 1; Y = 1) =
= 0, 15 + 0, 2 = 0, 35.
Если 1 < x ≤ 2 и y > 2, то F (x; y) = P (X = 1; Y = –1) + P (X = 1; Y = 1) +
+ P (X = 1; Y = 2) = 0, 6.
Если x > 2 и –1 < y ≤ 1, то F (x; y) = P (X = 1; Y = –1) + P (X = 2; Y = –1) =
= 0, 15 + 0, 2 = 0, 35.
Если x > 2 и 1 < y ≤ 2, то F (x; y) = P (X = 1; Y = –1) + P (X = 2; Y = –1) +
+ P (X = 1; Y = 1) + P (X = 2; Y = 1) = 0, 15 + 0, 2 + 0, 2 + 0, 1 = 0, 65.
Если x > 2 и y > 2, то F (x; y) = P (X = 1; Y = –1) + P (X = 2; Y = –1) +
+ P (X = 1; Y = 1) + P (X = 2; Y = 1) + P (X = 1; Y = 2) + P (X = 2; Y = 2) = 0, 15 + + 0, 2 + 0, 2 + 0, 1 + 0, 25 + 0, 1= 1.
Таким образом, функцию распределения данной системы дискретных случайных величин можно задать таблицей
| F (x; y) = | при | y ≤ –1 | –1 < y ≤ 1 | 1 < y ≤ 2 | y > 1 |
| x ≤ 1 | |||||
| 1 < x ≤ 2 | 0, 15 | 0, 35 | 0, 6 | ||
| x > 2 | 0, 35 | 0, 65 |
в) P (X ≤ Y)= P (X = 1; Y = 1) + P (X = 1; Y = 2) + P (X = 2; Y = 2) = 0, 2 +
+ 0, 25 + 0, 1 = 0, 55.
г) Условные вероятности значений СВ Y при X = x 2 найдем по формуле (1.63)
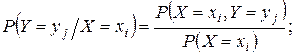
P (X = x 2) = (X = 2) = 0, 4;
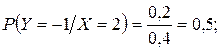
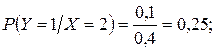
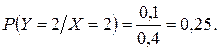
Таким образом условный закон распределения СВ Y при X = 2 имеет вид
| yj | –1 | ||
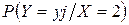
| 0, 5 | 0, 25 | 0, 25 |
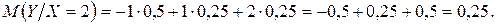
д) Так как безусловный и условный законы распределения СВ Y не совпадают, то случайные величины X и Y зависимы. (В этом можно было убедиться и другим способом: P (X = 2; Y = 1) =0, 1; P (X = 2) × P (Y = 1) =
= 0, 4 × 0, 3 = 0, 12; 0, 1 ¹ 0, 12).
е) Используя найденные законы распределения составляющих X и Y вычислим M (X) и M (Y):
M (X) = 1 × 0, 6 + 2 × 0, 4 = 1, 4; M (Y) = 1 × 0, 35 + 1 × 0, 3 + 2 × 0, 35 = 0, 65.
Точка (1, 4; 0, 65) – центр рассеивания двумерной случайной величины (X; Y).
ж) Так как случайные величины X и Y зависимы, то удобнее находить закон распределения случайной величины Z = XY по закону распределения двумерной СВ (X; Y).
Возможные значения случайной величины Z:
z 1 = –2, z 2 = –1, z 3 = 1, z 4 = 2, z 5 = 4.
Определим соответствующие им вероятности:
p 1 = P (Z = –2) = P (X = 2; Y = –1) = 0, 2;
p 2 = P (Z = –1) = P (X = 1; Y = –1) = 0, 15;
p 3 = P (Z = 1) = P (X = 1; Y = 1) = 0, 2;
p 4 = P (Z = 2) = P (X = 2; Y = 1) + P (X = 1; Y = 2)= 0, 1 + 0, 25 = 0, 35;
p 5 = P (Z = 4) = P (X = 2; Y = 2) = 0, 1.
Ряд распределения СВ Z имеет вид:
| zi | –2 | –1 | |||
| pi | 0, 2 | 0, 15 | 0, 2 | 0, 35 | 0, 1 |
з) Коэффициент корреляции rXY найдем по формуле (1.74)

используя для определения корреляционного момента KXY соотношение (1.72)
KXY = M (XY) – M (X) × M (Y).
M (XY) = M (Z) = –2 × 0, 2 – 1 × 0, 15 + 1 × 0, 2 + 2 × 0, 35 + 4 × 0, 1 = –0, 4 – 0, 15 +
+ 0, 2 + 0, 7 + 0, 4 = 0, 75.
(M (XY) можно также находить по формуле (1.73) 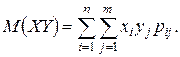 При этом M (XY) = 1(–1) × 0, 15 + 2(–1) × 0, 2 + 1 × 1 × 0, 2 + 2 × 1 × 0, 1 +
При этом M (XY) = 1(–1) × 0, 15 + 2(–1) × 0, 2 + 1 × 1 × 0, 2 + 2 × 1 × 0, 1 +
+ 1 × 2 × 0, 25 + 2 × 2 × 0, 1 = –0, 15 – 0, 4 + 0, 2 + 0, 2 + 0, 5 + 0, 4 = 0, 75.)
Так как M (X) =1, 4 и M (Y) = 0, 65, то KXY = 0, 75 – 1, 4 × 0, 65 = 0, 75 – 0, 91 =
= – 0, 16.
Вычисляем средние квадратические отклонения составляющих по формулам
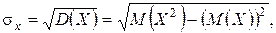
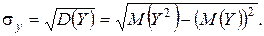
Так как законы распределения случайных величин X 2 и Y 2 имеют вид:
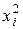
| и | 
| , | ||||
| pi | 0, 6 | 0, 4 | pj | 0, 65 | 0, 35 |
то M (X 2) = 1 × 0, 6 + 4 × 0, 4 = 0, 6 + 1, 6 = 2, 2;
D (X) = 2, 2 – (1, 4)2 = 2, 2 – 1, 96 = 0, 24;
M (Y 2) = 1 × 0, 65 + 4 × 0, 35 = 0, 65 + 1, 4 = 2, 05;
D (Y) = 2, 05 – (0, 65)2 = 2, 05 – 0, 4225 = 1, 5275;