
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальное, равномерное и показательное распределения 1 страница
|
|
Пример 1. Математическое ожидание нормально распределенной непрерывной СВ X M (X) = 6, а среднее квадратическое отклонение s(X) = 2.
Найти: 1) вероятность попадания значений СВ X в интервал (2; 9);
2) 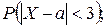
3) интервал, симметричный относительно a, в который попадают значения СВ X с вероятностью g = 0, 9642.
Решение. 1) Найдем вероятность попадания значений СВ X в интервал (2; 9).
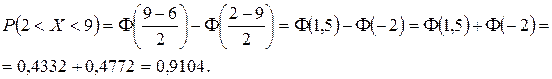
Значения функции Лапласа 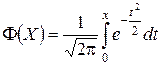 взяты из таблицы. Учтено свойство нечетности функции Ф(– X) = – Ф(X).
взяты из таблицы. Учтено свойство нечетности функции Ф(– X) = – Ф(X).
2) Определим вероятность 
Так как a = M (X) = 6 и s = s(X) = 2, то 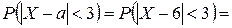
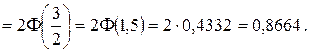
3) Найдем интервал, симметричный относительно a, в который попадают значения СВ X с вероятностью g = 0, 9642.
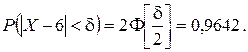 Из таблицы значений функции Лапласа находим
Из таблицы значений функции Лапласа находим 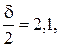 то есть d = 4, 2. Тогда интервал равен –4, 2 < X – 6 < 4, 2 и
то есть d = 4, 2. Тогда интервал равен –4, 2 < X – 6 < 4, 2 и
1, 8 < X < 10, 2.
Пример 2. Случайная величина Т (час.) – время безотказной работы прибора имеет показательное распределение. Найти вероятность того, что прибор проработает без ремонта не менее 600 часов, если среднее время безотказной работы приборов этого типа равно 400 часам.
Решение. M (T) = 400 час., следовательно, по формуле (1.46) 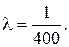 Так как для показательного распределения
Так как для показательного распределения 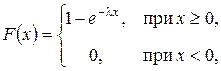 то
то 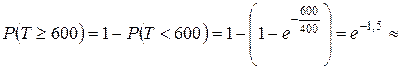 0, 2233.
0, 2233.
Пример 3. Случайная величина X распределена равномерно на отрезке [ a, b ]. Найти вероятность попадания случайной величины X на отрезок
[a, b], целиком содержащийся внутри отрезка [ a, b ].
Решение. Воспользуемся формулой  где плотность вероятности
где плотность вероятности 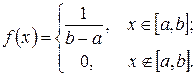
Тогда
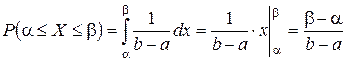 .
.
Таким образом 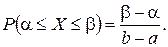
Пример 4. Электропоезда идут строго по расписанию с интервалом
20 мин. Найти вероятность того, что пассажир, подошедший к платформе, будет ожидать очередной электропоезд более 10 мин., а также среднее время ожидания.
Решение. X – время ожидания (мин.) электропоезда, можно считать равномерно распределенной случайной величиной с плотностью:
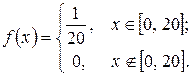
Тогда
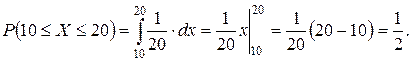
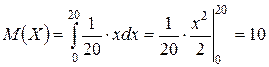 и это среднее время ожидания электропоезда.
и это среднее время ожидания электропоезда.
Пример 5. Автомат изготовливает втулки. Втулка считается годной, если отклонение X ее диаметра от проектного размера по абсолютной величине меньше 1мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением s = 0, 5 мм и математическим ожиданием a = 0, найти сколько будет годных втулок среди 100 изготовленных, а так же вероятность того, что отклонение от проектного размера будет не менее 0, 4 мм и не более 0, 8 мм.
Решение. Воспользуемся формулой () 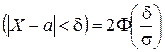 при d = 1, s = 0, 5 и a = 0.
при d = 1, s = 0, 5 и a = 0.
Получим
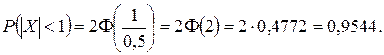
Отсюда следует, что примерно 95 втулок из 100 окажутся годными.
Для нахождения вероятности того, что отклонение от проектного размера будет не менее 0, 4 мм и не более 0, 8 мм воспользуемся формулой (1.54)
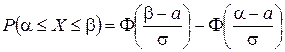 при a = 0, s = 0, 5, a = 0, 4, b = 0, 8.
при a = 0, s = 0, 5, a = 0, 4, b = 0, 8.
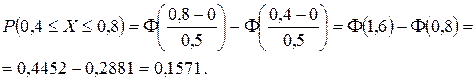
Значения функции Ф(x) находим по таблице.
Варианты заданий
ВАРИАНТ 1
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 1 | 0, 2 | 0, 3 | 0, 1 | 0, 3 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (8≤ X < 30). Построить многоугольник распределения и график F (x).
Задача 2. Каждый из стрелков стреляет по мишени один раз. Вероятность того, что первый, второй и третий стрелки попадут в мишень при одном выстреле, соответственно равны 0, 8; 0, 6 и 0, 9. Для
CB Х – общего числа попаданий в мишень при указанных условиях, составить ряд распределения и найти F (x), M (X), s(X) и D (X).
Задача 3. Вероятность появления некоторого события А в каждом опыте равна 0, 6. Требуется: 1) построить ряд распределения дискретной CB X – числа появлений события А в четырех независимых опытах; 2) оценить вероятность того, что в серии из 80 независимых опытов это событие появится не менее 60 раз.
Задача 4. Дискретная CB X задана рядом распределения:
| xi | –2 | –1 | |||||
| pi | 0, 05 | 0, 10 | 0, 15 | ? | 0, 15 | 0, 20 | 0, 10 |
Найти ряд распределения CB Y = –2 X 2 + 3, M (Y) и D (Y).
Задача 5. Непрерывная CB X задана функцией распределения
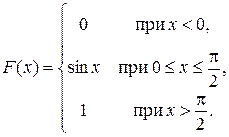
Найти: а) плотность распределения f (x); б) M (x); в) 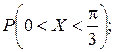 г) вероятность того, что в трех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу
г) вероятность того, что в трех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу 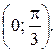
Задача 6. Задана функция 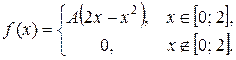
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 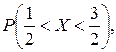 M (X) и D (X). Построить график F (x).
M (X) и D (X). Построить график F (x).
Задача 7. Заданы M (X) = 14 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность  ;
;
2) вероятность 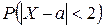 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 8385.
Задача 8. Шкала секундомера имеет цену деления 0, 2 с. Отсчет времени делается с точностью до целого деления с округлением в ближайшую сторону. Ошибку отсчета при указанных условиях можно считать равномерно распределенной случайной величиной.
Найти вероятность произвести по этому секундомеру отсчет времени с ошибкой а) менее 0, 05 с; б) не менее 0, 01 с и не более 0, 05 с.
ВАРИАНТ 2
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –2 | –1 | |||
| pi | 0, 2 | 0, 2 | 0, 1 | 0, 3 | 0, 2 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (–2 ≤ X < 5). Построить многоугольник распределения и график F (x).
Задача 2. В лотерее 100 билетов, из которых 10 выигрышных. Некто покупает 4 билета. Для СВ Х – числа выигрышных билетов среди тех, что будут куплены, составить ряд распределения и найти F (x), М (X), s(X).
Задача 3. Отчеты составляются независимо один от другого. Вероятность допустить ошибку при составлении каждого отчета равна 0, 3. Требуется: 1) построить ряд распределения CB X – числа отчетов с ошибками среди четырех составляемых; вычислить M (X), D (X) и s(X); 2) оценить вероятность того, что при составлении 50 отчетов будет равно 20 отчетов с ошибками.
Задача 4. Известно, что дискретная CB X можетпринимать только два значения x 1 = –2 и x 2 = 3 и ее математическое ожидание M (X) = 1, 5. Составить ряды распределения CB X и CB Z = 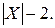 Найти F (z) и s(Z).
Найти F (z) и s(Z).
Задача 5. Непрерывная CB X задана функцией распределения
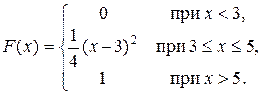
Найти: 1) плотность распределения f (x); 2) M (x) и D (X);
3) 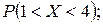 4) вероятность того, что в трех независимых испытаниях CB X ровно один раз примет значение, принадлежащее интервалу (1; 4).
4) вероятность того, что в трех независимых испытаниях CB X ровно один раз примет значение, принадлежащее интервалу (1; 4).
Задача 6. Задана функция 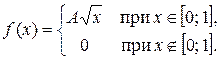
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 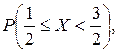 M (X), D (X). Построить график F (x).
M (X), D (X). Построить график F (x).
Задача 7. Заданы M (X) = 12 и s(X) = 2 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 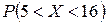 ;
;
2) вероятность 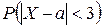 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 4515.
Задача 8. Случайная ошибка измерения некоторой детали подчинена нормальному закону с параметром s = 20 мм. Найти вероятность того, что: а) измерение детали произведено с ошибкой, не превосходящей по модулю 22 мм; б) ни в одном из двух произведенных измерений ошибка не превысит по модулю 22 мм.
ВАРИАНТ 3
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 3 | 0, 1 | 0, 1 | 0, 4 | 0, 1 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (1 ≤ X < 7). Построить многоугольник распределения и график F (x).
Задача 2. Из трех спортсменов, вошедших в молодежную сборную страны на соревнованиях по прыжкам в высоту, один может пройти квалифицированные старты с вероятностью 0, 9, второй с вероятностью 0, 8 и третий с вероятностью 0, 6. Для CB Х – количества спортсменов сборной, которые пройдут в следующий круг соревнований, составить ряд распределения и найти M (X), s(X).
Задача 3. Производится серия независимых выстрелов по цели. Вероятность попадания в цель при каждом выстреле равна 0, 8. Требуется: 1) построить ряд распределения CB X – числа попаданий при трех выстрелах; 2) оценить вероятность того, что при 100 выстрелах будет не менее 90 попаданий.
Задача 4. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –3 | –2 | –1 | ||
| pi | 0, 1 | 0, 2 | 0, 3 | 0, 2 | ? |
Найти ряд и функцию распределения CB Y = 2 X + 1, M (Y) и D (Y).
Задача 5. Непрерывная CB X задана функцией распределения
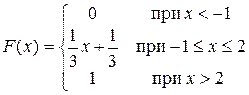
Найти: 1) плотность распределения f (x); 2) M (x) и D (X);
3) P (–2, 3 < X < 1, 5); 4) вероятность того, что в трех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу (–2, 3; 1, 5).
Задача 6. Задана функция 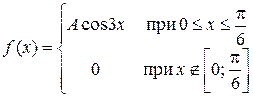
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 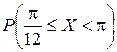 и M (X). Построить график F (x).
и M (X). Построить график F (x).
Задача 7. Заданы M (X) = 13 и s(X) = 4 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 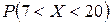 ;
;
2) вероятность 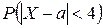 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9973.
Задача 8. Известно, что время ремонта телевизора есть случайная величина X, распределенная по показательному закону, при этом среднее время ремонта телевизора составляет две недели. Найти вероятность того, что на ремонт привезенного в мастерскую телевизора потребуется: а) менее 10 дней; б) от 9 до 12 дней.
ВАРИАНТ 4
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –10 | –5 | |||
| pi | 0, 1 | 0, 1 | 0, 4 | 0, 1 | 0, 3 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (–10≤ X < 1). Построить многоугольник распределения и график F (x).
Задача 2. У дежурного имеется 5 разных ключей от разных комнат. Вынув наудачу ключ, он пробует открыть дверь одной из комнат. Для дискретной CB X – числа попыток открыть дверь (проверенный ключ второй раз не используется) составить ряд распределения и найти F (x) и M (X).
Задача 3. Вероятность изготовления детали с заданными параметрами точности из стандартной заготовки для каждой детали равна 0, 8.
Требуется: 1) построить ряд распределения CB X – числа деталей с заданными точностными характеристиками, которые будут изготовлены из пяти стандартных заготовок; 2) оценить вероятность того, что будет изготовлено 70 деталей с заданными точностными характеристиками из 90 заготовок.
Задача 4. Заданы законы распределения независимых дискретных CB X и Y:
| xi | |||
| pi | ? | 0, 5 | 0, 2 |
| yi | ||
| pi | 0, 6 | ? |
Составить ряд распределения CB Z = Y – X. Найти M (Z) и D (Z).
Задача 5. Непрерывная CB X задана функцией распределения
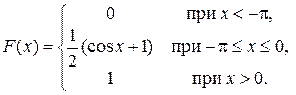
Найти: 1) плотность распределения f (x); 2) M (x); 3) 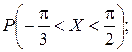 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу
4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу 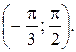
Задача 6. Задана функция 
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 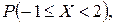 M (X) и D (X). Построить график F (x).
M (X) и D (X). Построить график F (x).
Задача 7. Заданы M (X) = 16 и s(X) = 2 нормально распределенной непрерывной СВ X. Найти:
1) вероятность  ;
;
2) вероятность 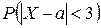 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9281.
Задача 8. Рост взрослого мужчины является СВ Х, распределенной по нормальному закону с параметрами а = 175 см и s = 10 см. Найти вероятность того, что рост случайно выбранного мужчины окажется: а) менее 180 см; б) не менее 170 см и не более 175 см.
ВАРИАНТ 5
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 2 | 0, 1 | 0, 4 | 0, 2 | 0, 1 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (40≤ X < 80). Построить многоугольник распределения и график F (x).
Задача 2. Мишень состоит из круга и двух концентрических колец. Попадание в круг дает 6 очков, в кольцо 2 дает 4 очка, а попадание в кольцо 3 дает два очка. Вероятности попадания в круг и кольца 2 и 3 соответственно равны 0, 2; 0, 3 и 0, 5. Для дискретной СВ Х – суммы выбитых очков в результате трех попаданий, составить ряд распределения и найти F (x), M (X), s(X).
Задача 3. Автоматическая линия состоит из n независимо работающих однотипных станков. Вероятность того, что станок потребует наладки в течение смены для каждого станка равна 0, 3. Требуется: 1) построить ряд распределения CB X – числа станков, которым потребуется наладка в течение смены, если n = 4; 2) оценить вероятность того, что за смену потребуют наладки 20 станков, если n = 100.
Задача 4. Совместное распределение дискретных CB X и Y задано таблицей:
| Y X | |||
| 0, 20 | 0, 15 | 0, 10 | |
| 0, 30 | 0, 20 | 0, 05 |
Составить закон распределения CB Z = Y + X. Найти M (Z) и D (Z).
Задача 5. Непрерывная CB X задана функцией распределения
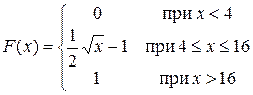
Найти: 1) плотность распределения f (x); 2) M (x) и D (X);
3) P (3 < X < 9); 4) вероятность того, что в четырех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу (3; 9).
Задача 6. Задана функция 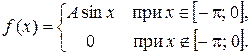
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 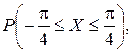 M (X). Построить график F (x).
M (X). Построить график F (x).
Задача 7. Заданы M (X) = 10 и s(X) = 4 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 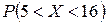 ;
;
2) вероятность 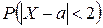 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 5161.
Задача 8. Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Случайная величина X – разница между временем, показываемым на табло и истинным временем имеет равномерное распределение. Найти вероятность того, что в некоторый момент времени часы укажут время, которое отличается от истинного: а) не менее, чем на 10 с и не более, чем на 25 с; б) не менее, чем на 25 с.
ВАРИАНТ 6
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –5 | –3 | –1 | ||
| pi | 0, 2 | 0, 2 | 0, 1 | 0, 4 | 0, 1 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (– 3≤ X < 1). Построить многоугольник распределения и график F (x).
Задача 2. В группе 12 студентов, из которых 5 живут в общежитии. По списку наудачу отбираются 4 студента. Для СВ Х – количества проживающих в общежитии студентов среди тех, кто будет отобран, составить ряд распределения и найти F (x), M (X) и D (X).
Задача 3. При изготовлении однотипных деталей на устаревшем оборудовании каждая деталь может оказаться бракованной с вероятностью 0, 1. Построить ряд распределения CB X – числа бракованных деталей среди четырех, которые будут изготовлены. Оценить вероятность того, что среди 900 изготовленных деталей бракованных будет три, если после смены оборудования вероятность брака для каждой детали станет равной 0, 002.
Задача 4. Дискретная CB X задана рядом распределения:
| xi | 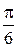
| 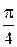
| 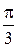
| 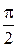
| p | |
| pi | 0, 15 | ? | 0, 25 | 0, 30 | 0, 10 | 0, 05 |
Найти ряд распределения CB Y = 2 sin2 X, M (Y) и D (Y).
Задача 5. Непрерывная CB X задана функцией распределения
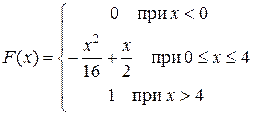
Найти: 1) плотность распределения f (x); 2) M (x), s(X); 3) P (1 < X < 3);
4) вероятность того, что в четырех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу (1; 3).
Задача 6. Задана функция 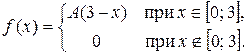
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 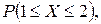 M (X) и D (X). Построить график F (x).
M (X) и D (X). Построить график F (x).
Задача 7. Заданы M (X) = 11 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 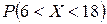 ;
;
2) вероятность 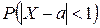 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9973.
Задача 8. Срок безотказной работы телевизора данной марки представляет собой случайную величину, распределенную по нормальному закону с параметрами а = 12 лет и s = 2 года. Найти вероятность того, что в телевизор проработает без ремонта: а) от 9 до 12 лет;
б) не менее 10 лет.
ВАРИАНТ 7
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 2 | 0, 1 | 0, 2 | 0, 3 | 0, 2 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (2≤ X < 10). Построить многоугольник распределения и график F (x).
Задача 2. Рабочий обслуживает 4 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего для первого станка равна 0, 7; для второго – 0, 75; для третьего – 0, 8; для четвертого – 0, 9. Для дискретной СВ Х – число станков, которые не потребуют внимания рабочего в течение часа, составить ряд распределения и найти F (x), M (X) и D (X).
Задача 3. Имеется n независимо работающих станков. Построить ряд распределения CB X – числа станков, работающих в данный момент времени, если n = 6, а вероятность того, что станок работает в данный момент времени равна 0, 9; вычислить M (X) и D (X). Оценить вероятность того, что на предприятии, у которого n = 180 и вероятность работы для каждого станка равна 0, 98, число работающих в данный момент станков будет не менее 170.
Задача 4. Заданы законы распределения независимых дискретных CB X и Y:
| xi | |||
| pi | 0, 3 | ? | 0, 5 |
| yi | –2 | –1 |
| pi | ? | 0, 4 |
Составить ряд распределения CB Z = XY + 2. Найти M (Z) и D (Z).