
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальное, равномерное и показательное распределения 2 страница
|
|
Задача 5. Непрерывная CB X задана функцией распределения
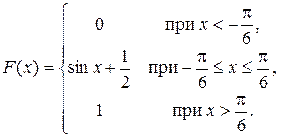
Найти: 1) плотность распределения f (x); 2) M (x); 3) P 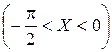 ; 4) вероятность того, что в трех независимых испытаниях CB X ровно один раз примет значение, принадлежащее интервалу
; 4) вероятность того, что в трех независимых испытаниях CB X ровно один раз примет значение, принадлежащее интервалу 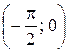 .
.
Задача 6. Задана функция 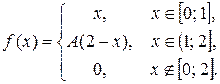
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 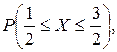 M (X) и D (X). Построить график F (x).
M (X) и D (X). Построить график F (x).
Задача 7. Заданы M (X) = 12 и s(X) = 2 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 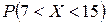 ;
;
2) вероятность 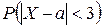 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 2358.
Задача 8. Время Т (в часах) до выхода из строя радиостанции подчинено показательному закону распределения с плотностью
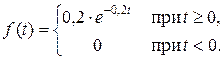
Найти вероятность того, что радиостанция сохранит работоспособность: а) от 1 до 5 часов работы; б) более 4 часов работы.
ВАРИАНТ 8
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –10 | –8 | –6 | ||
| pi | 0, 4 | 0, 1 | 0, 1 | 0, 2 | 0, 2 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность
P (– 10≤ X < 2). Построить многоугольник распределения и график F (x).
Задача 2. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0, 8. Стрелку выдаются патроны до тех пор, пока он не промахнется, но не более 5 патронов. Для СВ Х – числа выстрелов, которые произведет стрелок, составить ряд распределения и найти F (x), M (X) и D (X).
Задача 3. В техническом устройстве n независимо работающих элементов, каждый из которых за время T может отказать с вероятностью 0, 15. Требуется: 1) построить ряд распределения CB X – числа элементов, которые могут отказать за время T, если n = 5; вычислить М (X), D (X); 2) оценить вероятность того, что за время T откажут ровно 13 элементов, если n = 100.
Задача 4. Дискретная CB X может принимать два значения: x 1 и x 2, причем x 1 < x 2. Известно, что p 2 = 0, 6, М (X) = 0, 8, D (X) = 2, 16.Составить ряд распределения CB Z = 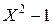 , найти M (Z) и D (Z).
, найти M (Z) и D (Z).
Задача 5. Непрерывная CB X задана функцией распределения

Найти: 1) плотность распределения f (x); 2) M (x) и D (X);
3) P (0 < X < 1); 4) вероятность того, что в пяти независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу (0; 1).
Задача 6. Задана функция
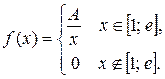
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x),  M (X) и D (X). Построить график F (x).
M (X) и D (X). Построить график F (x).
Задача 7. Заданы M (X) = 15 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 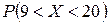 ;
;
2) вероятность 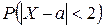 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 4039.
Задача 8. При штамповке деталей автоматом контролируется диаметр детали Х – нормально распределенная случайная величина с математическим ожиданием (проектная длина), равным 60 мм и средним квадратическим отклонением s = 3 мм. Найти вероятность того, что диаметр наудачу взятой детали окажется: а) более 61 мм; б) не менее 55 мм и не более 62 мм.
ВАРИАНТ 9
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 1 | 0, 1 | 0, 3 | 0, 3 | 0, 2 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (5≤ X < 11). Построить многоугольник распределения и график F (x).
Задача 2. На соревнованиях по прыжкам в длину каждому участнику предоставляют по три попытки. Для одного из участников первый прыжок может быть зачетным с вероятностью 0, 7, второй с вероятностью 0, 8, а третий – с вероятностью 0, 9. Для СВ Х – числа прыжков, которые войдут в зачет для этого прыгуна, составить ряд распределения и найти F (x), M (X) и D (X).
Задача 3. В среднем в двух случаях из пяти каждый из работающих приборов может исправно работать дольше установленного срока. Требуется: 1) построить ряд распределения дискретной CB X – числа приборов, работающих дольше установленного срока, среди четырех приборов, взятых наудачу из большой партии; вычислить М (X), D (X) и s(X); 2) оценить вероятность того, что из взятых наудачу из большой партии приборов, число таких, которые проработают дольше установленного срока, будет не менее 90 и не более 100.
Задача 4. Совместное распределение дискретных CB X и Y задано таблицей:
| Y X | |||
| 0, 15 | 0, 20 | 0, 10 | |
| 0, 20 | 0, 30 | 0, 05 |
Составить ряд распределения CB Z = 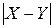 . Найти M (Z) и D (Z).
. Найти M (Z) и D (Z).
Задача 5. Непрерывная CB X задана функцией распределения
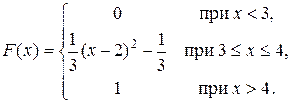
Найти: 1) плотность распределения f (x); 2) M (x) и D (X);
3) P (2 < X < 3, 5); 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу (2; 3, 5).
Задача 6. Задана функция
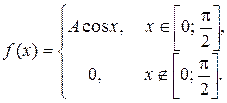
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 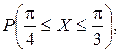 M (X) и D (X). Построить график F (x).
M (X) и D (X). Построить график F (x).
Задача 7. Заданы M (X) = 17 и s(X) = 4 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 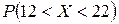 ;
;
2) вероятность 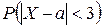 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9973.
Задача 8. Катера отплывают от пристани с интервалом 30 мин. Пассажир, не зная расписания, подходит к пристани в произвольный момент времени. Время ожидания можно считать непрерывной случайной величиной X, имеющей равномерное распределение. Найти вероятность того, что: а) 10 ≤ X ≤ 20; б) X ≥ 15.
ВАРИАНТ 10
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –4 | –2 | |||
| pi | 0, 2 | 0, 2 | 0, 3 | 0, 2 | 0, 1 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (– 4≤ X < 3). Построить многоугольник распределения и график F (x).
Задача 2. В группе 15 студентов, среди которых четверо имеют отличные оценки по философии. Преподаватель, не знакомый с группой, вызывает к доске трех человек. Для СВ Х – количества отличников по философии среди тех, кто будет вызван, составить ряд распределения и найти M (X) и D (X).
Задача 3. Вероятность обрыва нити на каждом из веретен ткацкого станка в произвольный момент времени равна 0, 2. Построить ряд распределения CB X – числа обрывов нити в произвольный момент времени у четырех веретен, вычислить M (X), D (X) и s(X).
Оценить вероятность того, что при обслуживании 800 веретен будет ровно три обрыва в произвольный момент времени, если вероятность обрыва для каждого веретена равна 0, 002.
Задача 4. Дискретная CB X задана рядом распределения:
| xi | –4 | |||
| pi | 0, 1 | 0, 4 | 0, 3 | ? |
Найти: ряд распределения 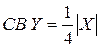 , F (y), M (Y) и s(Y).
, F (y), M (Y) и s(Y).
Задача 5. Непрерывная CB X задана функцией распределения

Найти: 1) плотность распределения f (x); 2) M (x) и D (X);
3) P (2 < X < 7); 4) вероятность того, что в четырех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу (2; 7).
Задача 6. Задана функция
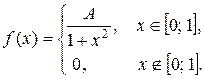
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 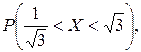 M (X) и D (X). Построить график F (x).
M (X) и D (X). Построить график F (x).
Задача 7. Заданы M (X) = 18 и s(X) = 5 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 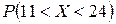 ;
;
2) вероятность 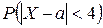 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 7699.
Задача 8. Случайное отклонение размера отливаемой болванки от стандарта подчинено нормальному закону с параметрами а = 45 дм,
s = 0, 2 дм. Найти вероятность того, что: а) размер выбранной наудачу болванки не менее 44, 8 дм и не более 45, 2 дм; б) среди двух выбранных наудачу болванок отклонение размера от стандарта не превзойдет 0, 2 дм.
ВАРИАНТ 11
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 4 | 0, 2 | 0, 1 | 0, 1 | 0, 2 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (4≤ X < 12). Построить многоугольник распределения и график F (x).
Задача 2. Охотник стреляет по дичи до первого попадания, но успевает сделать не более трех выстрелов. Вероятность попадания при каждом выстреле равна 0, 6. Для СВ Х – числа патронов, которые будут израсходованы, составить ряд распределения и найти M (X) и s(X).
Задача 3. Некоторое событие может появиться в каждом из независимых опытов с вероятностью 0, 7. Требуется: 1) построить ряд распределения CB X – числа непоявлений этого события в трех опытах, вычислить M (X), D (X) и s(X); 2) оценить вероятность того, что в 100 независимых опытах число появлений этого события будет менее 20.
Задача 4. Заданы законы распределения независимых дискретных CB X и Y:
| xi | |||
| pi | 0, 2 | ? | 0, 4 |
| yj | ||
| pj | 0, 4 | ? |
Составить закон распределения СВ Z = У – X. Найти F (z), M (Z) и D (Z).
Задача 5. Непрерывная CB X задана функцией распределения
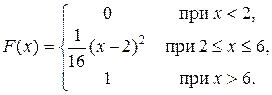
Найти: 1) плотность распределения f (x); 2) M (x) и D (X);
3) P (1 < X < 5); 4) вероятность того, что в трех независимых испытаниях CB X точно два раза примет значения, принадлежащие интервалу (1; 5).
Задача 6. Задана функция
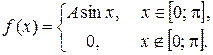
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 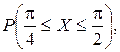 M (X). Построить график F (x).
M (X). Построить график F (x).
Задача 7. Заданы M (X) = 21 и s(X) = 6 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 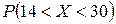 ;
;
2) вероятность 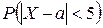 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 6872.
Задача 8. Время ожидания обслуживания у автозаправочной станции является случайной величиной Х, распределенной по показательному закону со средним временем ожидания 4 мин. Найти вероятность следующих событий: а) 2 мин. ≤ Х ≤ 6 мин.; б) Х ≥ 5 мин.
ВАРИАНТ 12
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –7 | –5 | –4 | –3 | |
| pi | 0, 1 | 0, 2 | 0, 3 | 0, 2 | 0, 2 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (– 5≤ X < 1). Построить многоугольник распределения и график F (x).
Задача 2. Испытуемый прибор состоит из четырех элементов. Вероятность отказа за время t элемента с номером i 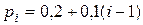 . Для СВ Х – числа элементов, которые откажут за время t, составить ряд распределения и найти F (x), M (X) и s(X).
. Для СВ Х – числа элементов, которые откажут за время t, составить ряд распределения и найти F (x), M (X) и s(X).
Задача 3. При каждом из нескольких независимых выстрелов вероятность попадания в цель равна 0, 7. Требуется: 1) построить ряд распределения CB X – числа непопаданий в цель при четырех выстрелах; вычислить M (X), D (X) и s(X); 2) оценить вероятность того, что при 80 выстрелах будет 30 непопаданий.
Задача 4. Дискретная CB X задана рядом распределения:
| xi | –2 | –1 | |||||
| pi | 0, 05 | ? | 0, 15 | 0, 25 | 0, 15 | 0, 20 | 0, 10 |
Составить ряд распределения 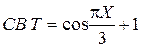 , найти M (T) и D (T).
, найти M (T) и D (T).
Задача 5. Непрерывная CB X задана функцией распределения

Найти: 1) плотность распределения f (x); 2) M (x); 3) 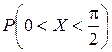 ; 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу
; 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу 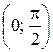 .
.
Задача 6. Задана функция
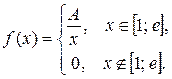
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x),  M (X) и s(X). Построить график F (x).
M (X) и s(X). Построить график F (x).
Задача 7. Заданы M (X) = 12 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность  ;
;
2) вероятность 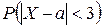 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9973.
Задача 8. Масса обитающих в Байкале омулей есть случайная величина X, подчиненная нормальному закону с параметрами а = 450 г (средний вес) и s = 20 г. Найти вероятность того, что масса выловленного омуля составит: а) более 400 г; б) от 390 г до 470 г.
ВАРИАНТ 13
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 1 | 0, 2 | 0, 3 | 0, 3 | 0, 1 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (12≤ X < 20). Построить многоугольник распределения и график F (x).
Задача 2. В коробке имеется 10 теннисных мячей, из которых 5 новых. Наудачу из коробки вынимают 4 мяча. Для СВ Х – числа новых мячей среди тех, что будут отобраны, составить ряд распределения и найти F (x) и s(X).
Задача 3. Проводятся несколько независимых расчетов. При проведении каждого расчета вероятность допустить ошибку равна 0, 2.
1) Построить ряд распределения CB X – числа расчетов без ошибок среди пяти проводимых; вычислить M (X), D (X) и s(X).
2) Оценить вероятность того, что при проведении 100 расчетов число расчетов без ошибок будет не менее 90.
Задача 4. Задан закон распределения вероятностей дискретной двумерной случайной величины:
| Y | X | |||
| 0, 05 | 0, 12 | 0, 08 | 0, 04 | |
| 0, 09 | 0, 30 | 0, 11 | 0, 21 |
Найти: 1) законы распределения составляющих X и Y; 2) закон распределения СВ Z = X + Y, M (Z) и D (Z).
Задача 5. Непрерывная CB X задана функцией распределения
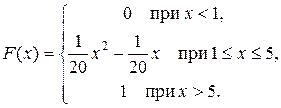
Найти: 1) плотность распределения f (x); 2) M (x) и s(X);
3) P (2 < X < 4); 4) вероятность того, что в четырех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу (2; 4).
Задача 6. Задана функция
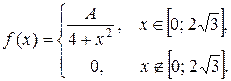
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти: F (x), 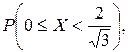 M (X) и s(X). Построить график F (x).
M (X) и s(X). Построить график F (x).
Задача 7. Заданы M (X) = 10 и s(X) = 2 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 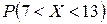 ;
;
2) вероятность 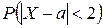 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9722.
Задача 8. Время работы сотового телефона без подзарядки – случайная величина, имеющая показательный закон распределения. Найти вероятность того, что телефон проработает без подзарядки: а) от 2 до 4 дней; б) более 3 дней, если среднее время работы телефона без подзарядки равно 4 дням.
ВАРИАНТ 14
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –8 | –4 | –2 | ||
| pi | 0, 2 | 0, 2 | 0, 2 | 0, 1 | 0, 3 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (–8≤ X < –2). Построить многоугольник распределения и график F (x).
Задача 2. Для контроля качества партии из 5 приборов производятся последовательные испытания приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Вероятность выдержать испытание для каждого прибора равна 0, 9. Для СВ Х – числа испытаний, которые будут произведены, составить ряд распределения и найти М (X) и s(X).
Задача 3. Вероятность оказаться бракованной для каждой из независимо изготовленных на производственном участке деталей равна 0, 05. Построить ряд распределения CB X – числа годных деталей среди пяти изготовленных; вычислить M (X) и s(X).
Оценить вероятность того, что среди 1000 производимых деталей окажутся ровно две бракованные, если вероятность оказаться бракованной для каждой детали будет равна 0, 003.
Задача 4. Дискретная CB X задана рядом распределения:
| xi | –2 | –1 | ||
| pi | 0, 2 | 0, 3 | ? | 0, 1 |
Найти: 1) ряд и функцию распределения 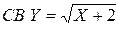 ; 2) M (Y) и D (Y).
; 2) M (Y) и D (Y).
Задача 5. Непрерывная CB X задана функцией распределения
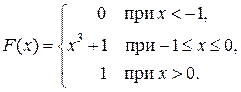
Найти: 1) плотность распределения f (x); 2) M (x) и s(X);
3) 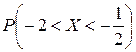 ; 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу
; 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу 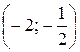 .
.
Задача 6. Задана функция 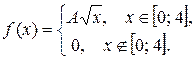
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 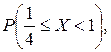 M (X) и D (X). Построить график F (x).
M (X) и D (X). Построить график F (x).
Задача 7. Заданы M (X) = 13 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 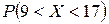 ;
;
2) вероятность 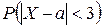 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 8664.
Задача 8. Один из размеров детали, произведенной станком с числовым программным управлением, есть случайная величина Х, подчиненная нормальному закону с параметрами а = 10 см и s = 0, 2 см. Найти вероятность того, что: а) размер произведенной детали будет отличаться от среднего по модулю не более, чем на s; б) размер произведенной детали будет не менее 9, 6 см и не более 10, 1 см.
ВАРИАНТ 15
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 1 | 0, 2 | 0, 3 | 0, 2 | 0, 2 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (5≤ X < 13). Построить многоугольник распределения и график F (x).
Задача 2. В партии из 8 деталей имеется 6 деталей первого сорта и 2 детали второго сорта. Наудачу, одна за другой без возращения в партию, отбираются детали до тех пор, пока не будет выбрана деталь первого сорта. Для СВ Х – числа отобранных при этом деталей второго сорта, составить ряд распределения и найти F (x), М (X) и s(X).
Задача 3. На участке независимо друг от друга работают n однотипных станков. Вероятность того, что станок потребует наладки в течение смены для каждого станка равна 0, 4.
1) Построить ряд распределения CB X – числа станков, которые не потребуют наладки в течение смены среди трех работающих; вычислить M (X), D (X) и s(X).
2) Оценить вероятность того, что число станков, которые не потребуют наладки в течение смены, будет не менее 50 и не более 70, если n = 100.