
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальное, равномерное и показательное распределения 4 страница
|
|
ВАРИАНТ 23
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 3 | 0, 1 | 0, 1 | 0, 1 | 0, 4 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (3≤ X < 13). Построить многоугольник распределения и график F (x).
Задача 2. В контрольную работу по математике включены задачи по четырем темам. Студент может решить задачи по каждой из первых двух тем с вероятностью 0, 8, по третьей теме с вероятностью 0, 6, а по четвертой – с вероятностью 0, 4. Для СВ Х – количества задач, которые будут решены студентом на контрольной работе, составить ряд распределения и найти F (x), M (X) и s(X).
Задача 3. Проверка нескольких документов ведется независимо друг от друга. Вероятность допустить ошибку при проверке одного документа для каждого документа равна 0, 1. Построить ряд распределения CB X – числа документов, в которых ошибка не будет обнаружена, среди трех проверяемых; вычислить M (X), D (X), s(X). Оценить вероятность того, что при проверке 40 документов будет ровно шесть проверенных с ошибкой.
Задача 4. Дискретная CB X задана рядом распределения:
| xi | –2 | –1 | ||||
| pi | ? | 0, 20 | 0, 30 | 0, 25 | 0, 10 | 0, 05 |
Найти ряд распределения CB 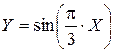 , M (Y) и D (Y).
, M (Y) и D (Y).
Задача 5. Непрерывная CB X задана функцией распределения
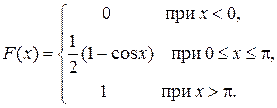
Найти: 1) плотность распределения f (x); 2) M (x); 3) вероятность того, что СВ Х примет значение в интервале 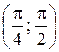 ; 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу
; 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу 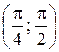 .
.
Задача 6. Задана функция 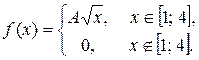
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти: F (x), P (0 ≤ X ≤ 2) M (X), D (X). Построить график F (x).
Задача 7. Заданы M (X) = 14 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 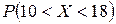 ;
;
2) вероятность 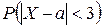 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9281.
Задача 8. Случайная ошибка измерения Х подчинена нормальному закону с параметрами а = 5, s = 0, 5. Найти вероятность того, что:
а) ошибка измерения не превосходит среднего квадратического отклонения; б) ошибка измерения не менее 0, 4 и не более 0, 9.
ВАРИАНТ 24
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –12 | –8 | –4 | –2 | |
| pi | 0, 1 | 0, 2 | 0, 1 | 0, 2 | 0, 4 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (–10≤ X < 0). Построить многоугольник распределения и график F (x).
Задача 2. Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0, 6; 0, 7 и 0, 8. СВ Х – количество элементов, которые откажут за время t. Для СВ Х составить ряд распределения и найти F (x), M (X) и s(X).
Задача 3. В исследовательской лаборатории имеются n однотипных независимо работающих приборов. Вероятность того, что прибор может потребовать настройки в течение часа, для каждого прибора равна 0, 2. Требуется: 1) построить ряд распределения CB X – числа приборов, которые могут потребовать настройки в течение часа, если n = 5; вычислить М (X), D (X), s(X); 2) оценить вероятность того, что число приборов, потребующих настройки в течение часа, будет ровно 20, если n = 80.
Задача 4. Совместное распределение дискретных CB X и Y задано рядом:
| Y X | |||
| 0, 15 | 0, 20 | 0, 10 | |
| 0, 20 | 0, 30 | 0, 05 |
Составить ряд распределения 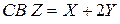 . Найти M (Z) и D (Z).
. Найти M (Z) и D (Z).
Задача 5. Непрерывная случайная величина X (CB X) задана функцией распределения F (x)
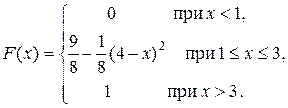
Найти: 1) плотность распределения f (x); 2) M (x) и D (X); 3) вероятность того, что СВ X примет значение принадлежащее интервалу
(0; 2); 4) вероятность того, что в четырех независимых испытаниях CB X четыре раза примет значения, принадлежащие интервалу (0; 2).
Задача 6. Задана функция 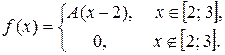
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), P (1 < X < 2, 5), M (X), D (X). Построить график F (x).
Задача 7. Заданы M (X) = 22 и s(X) = 4 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 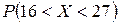 ;
;
2) вероятность 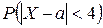 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9973.
Задача 8. Случайная величина Х, численно равная времени работы осциллографа (в часах) до выхода из строя, имеет плотность распределения
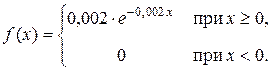
Найти среднее время работы осциллографа М (X), а также вероятность того, что осциллограф проработает от 400 до 600 часов.
ВАРИАНТ 25
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 2 | 0, 1 | 0, 2 | 0, 2 | 0, 3 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (6≤ X < 12). Построить многоугольник распределения и график F (x).
Задача 2. В команде 16 спортсменов, из которых 6 перворазрядников. Наудачу выбирают трех спортсменов. Для СВ Х – числа перворазрядников среди спортсменов, которые будут отобраны, составить ряд распределения и найти F (x), M (X) и s(X).
Задача 3. Мастерская производит однотипные изделия. Вероятность производства бракованного для каждого из них равна 0, 15. Построить ряд распределения CB X – возможного числа бракованных изделий среди трех, произведенных в мастерской; вычислить M (X), D (X), s(X). Оценить вероятность того, что будет одно бракованное изделие среди 800, если вероятность брака для каждого изделия равна 0, 001.
Задача 4. Дискретная CB X задана рядом распределения:
| xi | –2 | ? | |
| pi | ? | 0, 4 | 0, 4 |
Составить ряд распределения 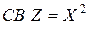 , если М (X) = 1, 2. Найти М (Z) и s(Z).
, если М (X) = 1, 2. Найти М (Z) и s(Z).
Задача 5. Непрерывная случайная величина X (СВ X) задана функцией распределения
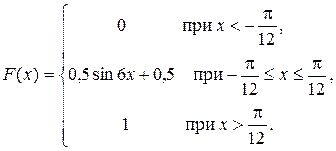
Найти: 1) плотность распределения f (x); 2) M (x); 3) вероятность того, что СВ X примет значение в интервале 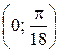 ; 4) вероятность того, что в трех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу
; 4) вероятность того, что в трех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу 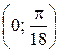 .
.
Задача 6. Задана функция 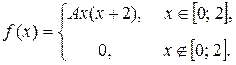
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти: F (x), M (X), D (X), P (– 1 ≤ X ≤ 1). Построить график F (x).
Задача 7. Заданы M (X) = 12 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 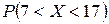 ;
;
2) вероятность 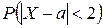 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9836.
Задача 8. Срок безотказной работы бытового прибора представляет собой случайную величину Х, распределенную по нормальному закону с параметрами а = 10 лет и s = 0, 9 года. Найти вероятность того, что прибор проработает: а) менее 9 лет; б) от 8 до 12 лет.
ВАРИАНТ 26
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –2 | –1 | |||
| pi | 0, 4 | 0, 2 | 0, 1 | 0, 1 | 0, 2 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (0≤ X < 5). Построить многоугольник распределения и график F (x).
Задача 2. Вероятность того, что студент найдет в библиотеке нужную ему книгу, для каждой из четырех доступных для студента библиотек равна 0, 4. Для СВ Х – числа библиотек, которые посетит студент, составить ряд распределения и найти F (x), M (X) и s(X).
Задача 3. Деталь с заданными параметрами из каждой заготовки можно изготовить с вероятностью 0, 6. Требуется: 1) построить ряд распределения CB X – возможного числа деталей с заданными параметрами среди тех, которые будут изготовлены из четырех заготовок; вычислить М (X), D (X), s(X); 2) оценить вероятность того, что будут изготовлены 65 деталей с заданными параметрами из 100 заготовок.
Задача 4. Случайный вектор (X, Y) распределен по закону, заданному таблицей:
| Y X | –1 | ||
| 0, 1 | 0, 2 | 0, 1 | |
| 0, 2 | 0, 3 | 0, 1 |
Найти ряд распределения СВ Z = X∙ Y, F (z) и М (Z).
Задача 5. Непрерывная случайная величина X (CB X) задана функцией распределения
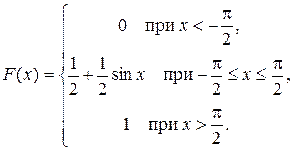
Найти: 1) плотность распределения f (x); 2) M (x); 3) вероятность того, что СВ X примет значение в интервале 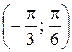 ; 4) вероятность того, что в трех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу
; 4) вероятность того, что в трех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу 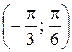 .
.
Задача 6. Задана функция 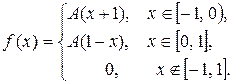 Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x),
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x), 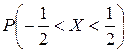 , M (X), D (X). Построить график F (x).
, M (X), D (X). Построить график F (x).
Задача 7. Заданы M (X) = 11 и s(X) = 4 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 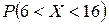 ;
;
2) вероятность 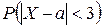 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 8064.
Задача 8. Цена деления шкалы рычажных весов, установленных в лаборатории, равна 1 г. При измерении массы химических компонентов производится измерение с точностью до целого деления с округлением в ближайшую сторону. Ошибка измерения является случайной величиной X, распределенный равномерно. Найти вероятность того, что ошибка измерения массы: а) не превысит 0, 2 г;
б) будет заключена между значениями 0, 2 г и 0, 4 г.
ВАРИАНТ 27
Задача 1. Дискретная случайная величина X (CB X) задана законом распределения:
| xi | |||||
| pi | 0, 1 | 0, 2 | 0, 3 | 0, 1 | 0, 3 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность
P (3≤ X < 12). Построить многоугольник распределения и график F (x).
Задача 2. Мишень состоит из внутреннего круга № 1 и двух концентрических колец с номерами 2 и 3. Попадание в круг № 1 дает 10 очков, в кольцо № 2 дает 5 очков, а попадание в кольцо № 3 штрафуется одним очком. Вероятности попадания в круг № 1 и кольца № 2 и № 3 соответственно равны 0, 5; 0, 3 и 0, 2. Для СВ Х – случайной суммы выбитых очков в результате трех попаданий, составить ряд распределения и найти F (x), M (X) и s(X).
Задача 3. С 13 до 14 часов каждый из n человек, независимо один от другого, может оказаться в столовой с вероятностью 0, 85.
Построить ряд и функцию распределения CB X – возможного числа посетителей столовой в этот промежуток времени, если
n = 5, вычислить М (X), D (X), s(X).
Оценить вероятность того, что число посетителей столовой в указанный промежуток времени будет равно 135, если n = 150 и вероятность для каждого из них оказаться в столовой с 13 до 14 часов равна 0, 94.
Задача 4. Известно, что дискретная CB X может принимать только два значения x 1 = –2 и x 2 = 3 и ее математическое ожидание M (X) = 1, 5. Составить ряды распределения CB X и CB Z =½ X ½ – 2. Найти F (z) и s(Z).
Задача 5. Непрерывная случайная величина X (CB X) задана функцией распределения
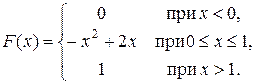
Найти: 1) плотность распределения f (x); 2) M (x), D (X);
3) 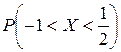 ; 4) вероятность того, что в четырех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу
; 4) вероятность того, что в четырех независимых испытаниях CB X ровно два раза примет значения, принадлежащие интервалу 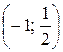 .
.
Задача 6. Задана функция 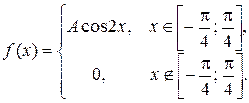
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой CB X. Найти F (x), 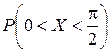 , M (X), D (X). Построить график F (x).
, M (X), D (X). Построить график F (x).
Задача 7. Заданы M (X) = 13 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 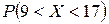 ;
;
2) вероятность 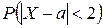 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9973.
Задача 8. Случайная величина Х распределена по показательному закону с параметром l = 0, 4. Найти дифференциальную функцию распределения f (x), а также вероятность попадания значений случайной величины Х в интервал [2, 5; 5].
ВАРИАНТ 28
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –20 | –10 | –2 | ||
| pi | 0, 2 | 0, 2 | 0, 3 | 0, 2 | 0, 1 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (–15< X ≤ 0). Построить многоугольник распределения и график F (x).
Задача 2. Студент знает 20 из 25 вопросов программы. На зачете студенту предлагается 5 вопросов. CB Х – число вопросов, на которые студент даст правильный ответ на зачете. Для СВ Х составить ряд распределения и найти F (x), M (X) и s(X).
Задача 3. Несколько анализаторов чистоты воздуха работают независимо друг от друга. Построить ряд и функцию распределения CB X – числа отказавших за промежуток времени T анализаторов из пяти имеющихся, если вероятность отказа для каждого анализатора равна 0, 1. Вычислить М (X), D (X), s(X). Оценить вероятность того, что за указанный промежуток времени могут отказать четыре анализатора из 900 работающих, если вероятность отказа любого из них равна 0, 001.
Задача 4. Задано распределение вероятностей двумерной случайной величины:
| X Y | |||
| 0, 17 | 0, 13 | 0, 25 | |
| 0, 10 | 0, 30 | 0, 05 |
Найти: 1) законы распределения составляющих X∙ и Y; 2) ряд распределения случайной величины Z = Y – X, M (z) и D (Z).
Задача 5. Непрерывная CB X задана функцией распределения
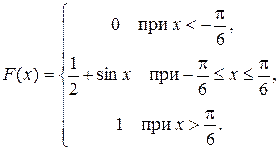
Найти: 1) плотность распределения f (x); 2) M (x);
3) 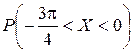 ; 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу
; 4) вероятность того, что в четырех независимых испытаниях CB X ровно три раза примет значения, принадлежащие интервалу 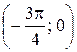 .
.
Задача 6. Задана функция 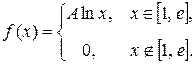
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F (x),  , M (X), D (X). Построить график F (x).
, M (X), D (X). Построить график F (x).
Задача 7. Заданы M (X) = 15 и s(X) = 4 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 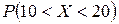 ;
;
2) вероятность 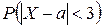 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9786.
Задача 8. Дальность полета снарядов артиллерийской установки есть случайная величина, подчиненная нормальному закону с параметрами а = 1500 м и s = 15 м. Найти вероятность того, что: а) отклонение от среднего значения не превысит среднего квадратического отклонения; б) отклонение будет не менее 10 м и не более 20 м.
ВАРИАНТ 29
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | |||||
| pi | 0, 1 | 0, 2 | 0, 2 | 0, 2 | 0, 3 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность
P (4≤ X < 12). Построить многоугольник распределения и график F (x).
Задача 2. Автомобиль на пути к месту назначения встретит 5 светофоров, каждый из которых пропустит его с вероятностью 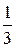 . СВ Х – число светофоров, которые пройдет автомобиль до первой остановки или до прибытия к месту назначения. Для CB X составить ряд распределения и найти F (x), M (X), D (X).
. СВ Х – число светофоров, которые пройдет автомобиль до первой остановки или до прибытия к месту назначения. Для CB X составить ряд распределения и найти F (x), M (X), D (X).
Задача 3. Каждый из n независимо работающих датчиков может отказать за время T с вероятностью 0, 1.
Построить ряд и функцию распределения CB X – возможного числа датчиков, которые откажут за время T, если n = 4; вычислить М (X), D (X), s(X).
Оценить вероятность того, что при n = 300 за время T может отказать ровно 25 датчиков.
Задача 4. Дискретная CB X может принимать только два значения X 1 и X 2, причем X 1 < X 2. Известно, что P 1 = 0, 3, M (X) = 2, 4 и D (X) = 0, 84. Найти ряд распределения CB X. Составить ряд распределения CB Z =2 X – 5, найти M (Z) и D (Z).
Задача 5. Непрерывная случайная величина X (CB X) задана функцией распределения
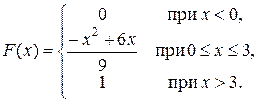
Найти: 1) плотность распределения f (x); 2) M (x), D (X); 3) P (1 < X < 2); 4) вероятность того, что в четырех независимых испытаниях CB X четыре раза примет значения, принадлежащие интервалу (1, 2).
Задача 6. Задана функция 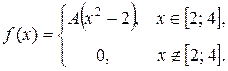
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой CB X. Найти F (x), P (1 < X < 3), M (X), D (X). Построить график F (x).
Задача 7. Заданы M (X) = 16 и s(X) = 4 нормально распределенной непрерывной СВ X. Найти:
1) вероятность 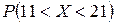 ;
;
2) вероятность 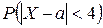 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 5761.
Задача 8. Ошибка Х измерения, производимого прибором, есть случайная величина, распределенная нормально. Систематической ошибки прибор не имеет, s = 0, 01. Найти вероятность следующих событий: а) ç Х ÷ ≤ s; б) –0, 02 ≤ Х ≤ 0.
ВАРИАНТ 30
Задача 1. Дискретная случайная величина X (CB X) задана рядом распределения:
| xi | –10 | –6 | –2 | ||
| pi | 0, 2 | 0, 1 | 0, 4 | 0, 2 | 0, 1 |
Найти: 1) функцию распределения F (x); 2) числовые характеристики: математическое ожидание М (X), дисперсию D (X), среднее квадратическое отклонение s(X), моду M 0(Х); 3) вероятность P (–7≤ X < 7). Построить многоугольник распределения и график F (x).
Задача 2. Нужная студенту для написания реферата информация содержится на трех сайтах. Вероятность того, что студент сможет найти эту информацию в течении t минут для каждого из сайтов соответственно равна 0, 6; 0, 5; 0, 8. CB Х – количество сайтов, на которых студент найдет нужную ему информацию, если на каждом из сайтов он будет проводить поиск не более чем t минут. Для СВ Х составить ряд распределения и найти F (x), M (X), D (X).
Задача 3. Каждый из анализаторов газовой среды может проработать дольше установленного срока в среднем в трех случаях из четырех.
Построить ряд и функцию распределения CB X – числа анализаторов, которые смогут проработать дольше установленного срока, среди шести случайно отобранных из большой партии; вычислить M (X), D (X), s(X).
Оценить вероятность того, что из 150 взятых случайно анализаторов число работающих дольше установленного срока будет не менее 100.
Задача 4. Дискретная CB X задана рядом распределения:
| xi | –1 | |
| pi | ? | 0, 6 |
CB Y – число появлений события А в серии из двух независимых испытаний, в каждом из которых P (A) = 0, 4.Составить ряд распределения CB Z = X + Y. Найти М (Z) и D (Z).
Задача 5. Непрерывная случайная величина X (СВ X) задана функцией распределения
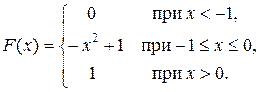
Найти: 1) плотность распределения f (x); 2) M (x); 3) P (–2 < X < – 0, 5); 4) вероятность того, что в трех независимых испытаниях CB X ровно 2 раза примет значения, принадлежащие интервалу (–2; –0, 5).
Задача 6. Задана функция 
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти: F (x), 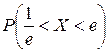 , M (X), D (X). Построить график F (x).
, M (X), D (X). Построить график F (x).
Задача 7. Заданы M (X) = 17 и s(X) = 3 нормально распределенной непрерывной СВ X. Найти:
1) вероятность  ;
;
2) вероятность 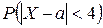 ;
;
3) симметричный относительно a интервал, в который попадают значения CB Х с вероятностью g = 0, 9973.
Задача 8. Случайная величина Х – время безотказной работы лампочки подчинена показательному закону распределения, причем среднее время работы лампочки 800 часов. Найти вероятность того, что: а) лампочка проработает от 400 до 700 часов; б) лампочка проработает более 600 часов.