Биномиальное распределение. Дискретная СВ X распределена по биномиальному закону, если она принимает значения 0, 1, 2, , n с вероятностями:

Дискретная СВ X распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, n с вероятностями:

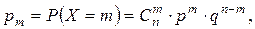(1.33)

где 0 < p < 1, q = 1 – p, m = 0, 1, …, n.

Из схемы Бернулли следует, что СВ X – число появлений события А в серии из n независимых опытов, в каждом из которых событие А может появиться с вероятностью p, имеет биномиальное распределение. Для
СВ X, имеющей биномиальное распределение с параметрами p и n,

M (X) = np, D (X) = npq, (1.34)

где q = 1 – p.

Следует отметить, что гипергеометрическое распределение при n малых по сравнению с N (практически при n < 0, 1 N) приближается к биномиальному распределению с параметрами n и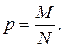

Замечание 1. Для вычисления 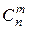при достаточно больших n и m применима формула Стирлинга:

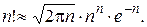
Замечание 2. Для биномиальных вероятностей справедлива рекуррентная формула:

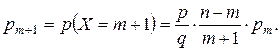
Замечание 3. Наиболее вероятное число успехов K ₀ в серии из n независимых испытаний удовлетворяет неравенству:

np – q ≤ K ₀ < np + p.