Дисперсия и среднее квадратичное отклонение

Дисперсией СВ X называется математическое ожидание квадрата отклонения этой СВ от ее математического ожидания.

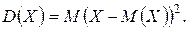(1.18)

Дисперсия характеризует разброс значений СВ X относительно ее математического ожидания. Из определения дисперсии следуют формулы для ее вычисления.

Для дискретной СВ X дисперсия вычисляется по формуле

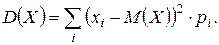(1.19)

Для непрерывной СВ X дисперсия находится по формуле

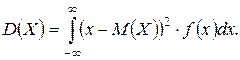(1.20)

С использованием свойств математического ожидания доказывается другая формула для нахождения дисперсии, которая удобна для практического применения:

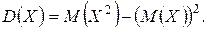(1.21)

Это соотношение позволяет записать формулы для вычисления дисперсии в другом виде:

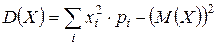для дискретной СВ X;

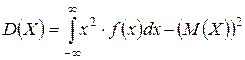для непрерывной СВ X.

Свойства дисперсии

1) D (с) = 0, где с = const.

2) M (с × X) = c ² × D (X), где с = const.

3) Для независимых СВ X и СВ Y

D (X + Y) = D (X) + D (Y).

4) Для независимых СВ X и СВ Y

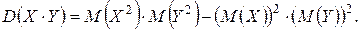
Средним квадратическим отклонением СВ X называется квадратный корень из ее дисперсии

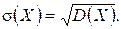(1.22)