
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дискретные случайные величины. Если множество возможных значений случайной величины конечно или счетно, то такая СВ называется дискретной
|
|
Если множество возможных значений случайной величины конечно или счетно, то такая СВ называется дискретной, ее значения могут быть перечислены и распределены в порядке возрастания.
СВ X – число попаданий в мишень при трех выстрелах – дискретна. Ее возможные значения: 0, 1, 2, 3. Другая случайная величина T – время безотказной работы прибора – не является дискретной, так как ее возможные значения целиком заполняют некоторый промежуток числовой прямой.
Простейшей формой закона распределения дискретной случайной величины Х является ряд распределения – таблица, в верхней строке которой перечислены все возможные значения x 1, x 2, …, xn или x 1, x 2, …, xi, … в порядке их возрастания, а в нижней – соответствующие им вероятности p 1, p 2, …, pi, …
| xi | x 1 | x 2 | … | xn |
| pi | p 1 | p 2 | … | pn |
(1.2)
или
| xi | x 1 | x 2 | … | xi | … |
| pi | p 1 | p 2 | … | pi | … |
(1.3)
где pi = P (X = xi). (1.4)
Так как события (X = x 1), (X = x 2)… несовместны и образуют полную группу событий, то сумма их вероятностей равна 1
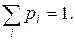 (1.5)
(1.5)
Закон распределения дискретной СВ можно задать графически, если на оси абсцисс отложить возможные значения СВ X, а на оси ординат - вероятности принятия случайной величиной этих значений. Ломаную, соединяющую последовательно точки (x 1, p 1), (x 2, p 2) … называют многоугольником распределения.
Схематический вид многоугольника распределения СВ X, принимающей конечное множество значений { x 1, x 2, …, xn } изображен на рисунке 1.
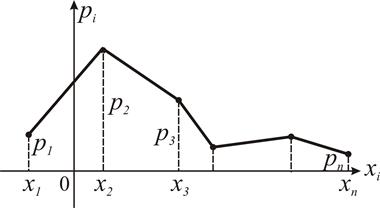
Рис. 1