
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывные и смешанные случайные величины
|
|
Многие случайные величины не являются дискретными, например: время безотказной работы прибора, погрешность измерения некоторой величины, расстояние от точки попадания до центра мишени, дальность обнаружения объекта радиолокатором. У всех этих СВ множество возможных значений, совпадает с некоторым промежутком числовой прямой.
Если функция распределения F (x) СВ X при любом x непрерывна и, кроме того, имеет производную 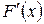 везде, кроме, может быть, отдельных точек разрыва первого рода, то случайная величина называется непрерывной.
везде, кроме, может быть, отдельных точек разрыва первого рода, то случайная величина называется непрерывной.
Если функция распределения F (x) на некоторых участках непрерывно возрастает, а в отдельных точках имеет разрывы I рода, то случайная величина называется смешанной. Функция F (x) для смешанной случайной величины, как и для дискретной, непрерывна слева.
Для непрерывной СВ X вероятность принятия этой величиной каждого отдельного значения равна нулю
P (X = x) = 0 (1.9)
и справедливо утверждение
P (a ≤ X < b) = P (a < X < b) = P (a < X ≤ b) = P (a ≤ X ≤ b) = F (b) – F (a). (1.10)
Для смешанной случайной величины вероятность принятия этой величиной каждого отдельного значения, принадлежащего участку непрерывности F (x), также равна нулю, а вероятность принятия случайной величиной каждого из тех значений x 1, x 2, …, в которых функция F (x) совершает скачки, численно равна значениям соответствующих скачков.
Плотностью распределения вероятности (или плотностью распределения или дифференциальной функцией распределения) непрерывной СВ X называется такая неотрицательная кусочно-непрерывная функция f (x) (PX (x)), что при любых x Î R выполняется равенство
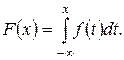 (1.11)
(1.11)
Для любой непрерывной СВ существует плотность распределения. Отметим важные свойства плотности распределения:
1) 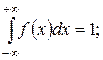 (1.12)
(1.12)
2) 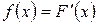 (1.13)
(1.13)
в точках непрерывности 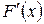 .
.
Для непрерывной СВ X с плотностью распределения f (x)
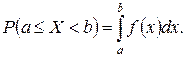 (1.14)
(1.14)