Теории пластичности

Третья теория прочности – теория наибольших касательных напряжений (теория Кулона).

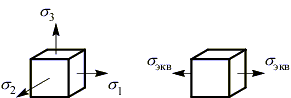
Критерий равнопрочности: напряженных состояния равнопрочны по наступлению недопустимых пластических деформаций, если у них равны наибольшие касательные напряжения

.

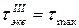По формуле (2.2) касательное напряжение в случае плоского напряженного состояния определяется как:

,

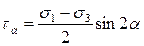из которой следует, что

.

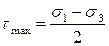При одноосном напряженном состояни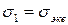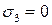и , , и

.

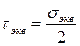Приравнивая правые части полученных выражений, получим эквивалентное напряжение по третьей теории

.

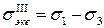Для случая плоского напряженного состояния, когда нормальное напряжение на одной из площадок равно нулю (изгиб с кручением), выразив главные напряжения через напряжения на произвольной площадке, условие прочности принимает вид:

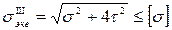. (2.9)

Третья теория используется при расчете элементов конструкций, изготовленных из пластичных материалов. Ее недостатком является неучет главного напряжения σ ₂.

Четвертая теория прочности – теория удельной потенциальной энергии формоизменения – энергетическая теория (теория Мизеса – Генки).

Критерий равнопрочности: напряженные состояния равнопрочны по наступлению недопустимых пластических деформаций, если у них равны удельные потенциальные энергии формоизменения:

.

Используя приведенное в разделе 8.1.5 выражение для потенциальной энергии изменения формы (8.1) для одноосного и объемного напряженного состояния, получим

,

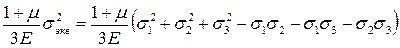откуда эквивалентное напряжение по четвертой теории

.

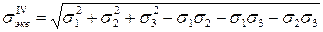Для случая плоского напряженного состояния ():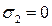

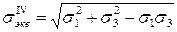. (2.10)

Выражая главные напряжения через напряжения на произвольных площадках для плоского напряженного состояния, когда на одной из площадок нормальное напряжение равно нулю, получим:

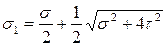и .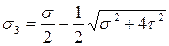

Подставляя полученные выражения в формулу (8.6), условие прочности можно записать в виде:

.

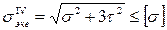Энергетическая теория хорошо согласуется с экспериментальными данными (лучше, чем третья теория), и широко используется для пластичных материалов.