
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства плотности распределения
|
|
- Плотность распределения неотрицательна, т.е.
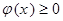 при всех х.
при всех х. - Интеграл от плотности распределения на всей числовой прямой равен 1, т.е.
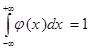 .
.
(Данное свойство называется условием нормировки плотности распределения.)
Доказательство. Предположим противное: пусть найдется такой отрезок 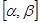 , что плотность распределения
, что плотность распределения 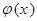 отрицательна на этом отрезке. Тогда (см. свойства определенного интеграла) имеем
отрицательна на этом отрезке. Тогда (см. свойства определенного интеграла) имеем

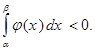
Но, по определению плотности распределения, интеграл, стоящий в левой части последнего неравенства равен 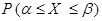 . Так как вероятность события не может быть отрицательной, приходим к противоречию, что доказывает справедливость свойства 1.
. Так как вероятность события не может быть отрицательной, приходим к противоречию, что доказывает справедливость свойства 1.
По определению плотности распределения,
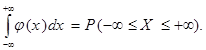
Но событие 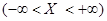 является достоверным, поэтому его вероятность равна 1. Тем самым доказано свойство 2.
является достоверным, поэтому его вероятность равна 1. Тем самым доказано свойство 2.