
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства функции распределения
|
|
- Функция распределения является неубывающей функцией.
- Область значений:
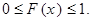
- Асимптотические свойства:
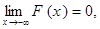
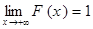 (другими словами, прямые у =0 и у =1 являются асимптотами (левой и правой соответственно) графика y = F (x)).
(другими словами, прямые у =0 и у =1 являются асимптотами (левой и правой соответственно) графика y = F (x)). - Вероятность того, что в произвольном испытании значение случайной величины Х будет принадлежать полуинтервалу
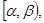 где
где 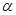 и
и 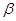 – произвольные числа, вычисляется по формуле
– произвольные числа, вычисляется по формуле
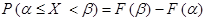 .
.
Доказательство. Значение функции распределения равна вероятности соответствующего события, но область значений вероятности есть отрезок 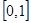 – тем самым доказано свойство 2.
– тем самым доказано свойство 2.
Используя определение функции распределения, получаем 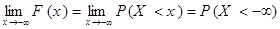 . Но произвольное значение случайной величины принадлежит числовой прямой, поэтому событие
. Но произвольное значение случайной величины принадлежит числовой прямой, поэтому событие 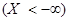 является невозможным. Вероятность невозможного события равна нулю (см. § 1.3), поэтому
является невозможным. Вероятность невозможного события равна нулю (см. § 1.3), поэтому 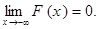
Аналогично, учитывая, что событие  является достоверным, а вероятность такого события равна 1, получаем
является достоверным, а вероятность такого события равна 1, получаем 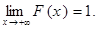
Нетрудно видеть, что
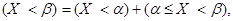
причем события правой части этого равенства несовместны. Принимая во внимание определение функции распределения и теорему сложении вероятностей для несовместных событий, получаем
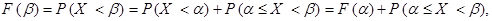
что равносильно свойству 4.
Доказательство свойства 1 мы оставляем читателю в качестве упражнения (указание: используйте рассуждении от противного и свойство 4).