
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Арифметические операции над случайными величинами
|
|
Определение. Случайные величины Х и Y называются равными, если их законы распределения точно совпадают, и для произвольного числа 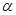 справедливо равенство:
справедливо равенство: 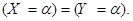
Пример. Пусть законы распределения случайных величин Х и Y имеют вид:
| Y: | 
| . | ||

| 0, 5 | 0, 5 |
| X: | 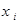
| ||

| 0, 5 | 0, 5 |
Эти случайные величины равны, если дополнительно справедливы равенства 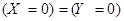 и
и 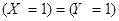 , т.е. случайная величина Х принимает значение 0
, т.е. случайная величина Х принимает значение 0
тогда и только тогда, когда случайная величина Y принимает значение 0, и аналогично со значением 1.
Произвольная случайная величина допускает умножение на число. Действительно, пусть закон распределения случайной величины Х имеет вид:
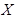 : :
| 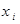
| 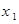
| 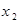
| … | 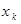
|

| 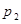
| 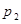
| … | 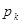
|
и 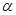 – некоторое число.
– некоторое число.
Определение. Случайной величиной 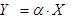 называется такая случайная величина, закон распределения которой имеет вид:
называется такая случайная величина, закон распределения которой имеет вид:
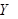 : :
| 
| 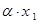
| 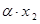
| … | 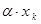
|

| 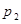
| 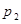
| … | 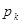
|
Пример. Пусть закон распределения случайной величины Х имеет вид:
| Х: | 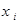
| |||
 
| 0, 16 | 0, 48 | 0, 36 |
и 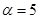 ,
, 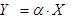 . Тогда закон распределения
. Тогда закон распределения 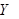 :
:
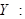
| 
| |||
 
| 0, 16 | 0, 48 | 0, 36 |
Можно придумать, например, следующую интерпретацию данному примеру. Заметим, что Х – биномиально распределена с параметрами 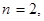
 . Пусть Х – число попаданий в мишень при 2-х выстрелах, при каждом из которых попадание случается с вероятностью 0, 6, и дополнительно известно, что за каждое попадание стрелку выплачивается вознаграждение в размере 5 ден. ед. Тогда Y – заработок стрелка.
. Пусть Х – число попаданий в мишень при 2-х выстрелах, при каждом из которых попадание случается с вероятностью 0, 6, и дополнительно известно, что за каждое попадание стрелку выплачивается вознаграждение в размере 5 ден. ед. Тогда Y – заработок стрелка.
Определение. Случайные величины Х и Y называются независимыми, если для любых i и j события 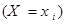 и
и 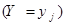 – независимы.
– независимы.
Пример. Пусть из коробки, в которой – 6 белых и 8 красных шаров, извлекается 1 шар. Рассмотрим случайные величины Х – число белых шаров, Y – число красных шаров из извлеченных. События, например, 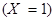 и
и 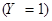 – несовместны, а поэтому – зависимы (см. § 1.6). Следовательно, и случайные величины Х и Y зависимы.
– несовместны, а поэтому – зависимы (см. § 1.6). Следовательно, и случайные величины Х и Y зависимы.
Определение. Суммой (разностью, произведением) случайных величин Х и Y называется такая случайная величина 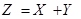 (
(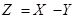 ,
, 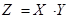 ), которая принимает значение
), которая принимает значение 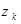 в некотором испытании, если значения
в некотором испытании, если значения 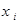 и
и 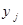 случайных величин Х и
случайных величин Х и 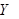 в этом испытании таковы, что
в этом испытании таковы, что 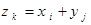 (
(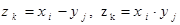 ).
).
Пример. Пусть заданы законы распределения независимых случайных величин Х и Y:
| Х: | 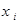
| Y: | 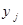
| ||||

| 0, 4 | 0, 6 | 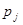
| 0, 2 | 0, 8 |
Составить закон распределения случайной величины 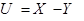 .
.
Решение. Удобно использовать вспомогательную таблицу вида:
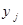 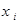
| ||
| –1 |
в каждой из центральных клеток которой записаны соответствующие произведения случайных величин X и Y. Такая таблица показывает, какие значения принимает случайная величина U и когда она принимает эти значения. Так 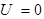 тогда и только тогда, когда
тогда и только тогда, когда 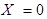 и
и  или
или 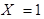 и
и 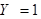 . Поэтому
. Поэтому
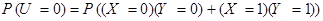 .
.
Применяя теорему сложения вероятностей для несовместных событий, теорему умножения вероятностей – для независимых событий (по условию, случайные величины 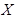 и
и 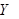 – независимы), получаем
– независимы), получаем
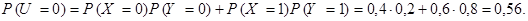
Для наступления каждого из двух оставшихся значений случайной величины U (-1 и 1) имеется по одной возможности. Например,  тогда и только тогда, когда
тогда и только тогда, когда 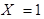 и
и  . Тогда получаем:
. Тогда получаем:
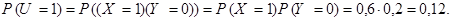
Аналогично,
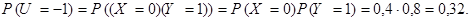
Окончательно, закон распределения случайной величины U имеет вид:
| U: | 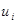
| –1 | ||
 
| 0, 32 | 0, 56 | 0, 12 |
Упражнение. Составить законы распределения случайных величин 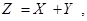


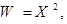
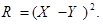
Ответ.
| Z: | 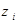
| V: | 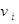
| |||||

| 0, 08 | 0, 44 | 0, 48 | 
| 0, 52 | 0, 48 |
| W: | 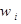
| R: | 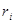
| ||||

| 0, 4 | 0, 6 | 
| 0, 56 | 0, 44 |
Заметим, что закон распределения случайной величины Z фактически найден в примере § 3.1 о двух стрелках. Действительно, исходные независимые случайные величины X и Y данной задачи могут быть интерпретированы как числа попаданий в мишень первого и второго стрелка из § 3.1. Тогда 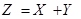 – общее число попаданий, и закон распределения этой случайной величины и найден в упомянутом примере.
– общее число попаданий, и закон распределения этой случайной величины и найден в упомянутом примере.