
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формула Пуассона (редких событий)
|
|
Теорема. Пусть произведено n повторных независимых испытаний, в каждом из которых некоторое событие А наступает с вероятностью p, причем
а) число испытаний достаточно велико (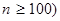 ;
;
б) 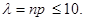
Тогда вероятность 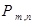 того, что в этих n испытаниях событие А наступит
того, что в этих n испытаниях событие А наступит 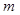 раз, вычисляется по следующей приближенной формуле
раз, вычисляется по следующей приближенной формуле
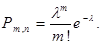
Эта формула и называется формулой Пуассона (редких событий).
Пример. По каналу связи передано 1000 сигналов. Вероятность ошибки при передаче каждого из сигналов равна 0, 005. Найти вероятность того, что неверно передано:
а) 7 сигналов;
б) не менее 4-х сигналов.
Решение. а) Воспользуемся формулой Пуассона, т.к. условия ее применимости в данном случае выполнены: число испытаний достаточно велико 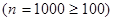 и
и 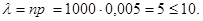 Искомое значение
Искомое значение 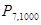 найдем по таблице функции Пуассона при
найдем по таблице функции Пуассона при 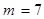 и
и 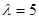 (см. учебник Н.Ш. Кремера, с.556):
(см. учебник Н.Ш. Кремера, с.556): 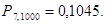
б) Требуется найти 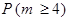 , где m – число неверно принятых сигналов. Так как
, где m – число неверно принятых сигналов. Так как 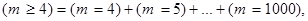 то
то 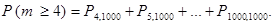
Искать каждое из слагаемых этой суммы и затем выполнять суммирование – такое решение не представляется рациональным из-за большого числа слагаемых и потому, что таблица функции Пуассона не дает искомых значений с требуемой в данном случае точностью. Воспользуемся переходом к противоположному событию: 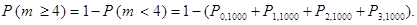
Находя вероятности из правой части последнего равенства по таблице функции Пуассона, окончательно получаем
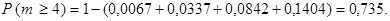
Домашнее задание: 2.20, 2.22б.