
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Классическое определение вероятности
|
|
Определение. Пусть некоторое испытание имеет n исходов, причем эти исходы
а) попарно несовместимы;
б) единственно возможны;
в) равновозможны
и наступлению события А благоприятствует 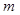 исходов из
исходов из 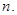 Тогда вероятность
Тогда вероятность 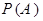 наступления события А (в одном испытании) определяется по формуле
наступления события А (в одном испытании) определяется по формуле
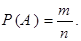
Пример. В коробкеимеется 10 хороших деталей и 5 бракованных. Наудачу из коробки извлекается одна деталь. Найти вероятность наступления события А – извлеченная деталь – хорошая.
Решение. Общее число исходов 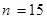 равно полному числу деталей в коробке. Извлечению хорошей детали благоприятствует
равно полному числу деталей в коробке. Извлечению хорошей детали благоприятствует 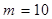 исходов из общего числа (число хороших деталей). Тогда
исходов из общего числа (число хороших деталей). Тогда
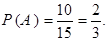
Пример. Одновременно бросаются три монеты. Найти вероятность того, что на двух из них выпадет “орел”.
Решение. Для удобства будем предполагать, что монеты некоторым образом занумерованы.Единичным исходом здесь является совокупный результат по трем монетам (другими словами, для того, чтобы задать единичный исход, надо сказать, что выпало на первой монете, на второй и на третьей). Перечислим возможные исходы (см. Таблицу 1, в которой выпадение “орла” на соответствующей монете обозначено буквой “О”, “решки” – “Р”). Видно, что общее число 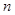 исходов равно 8. Число
исходов равно 8. Число 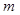 благоприятствующих исходов равно 3 – это исходы с номерами 2, 3, 5 Таблицы 1. Тогда
благоприятствующих исходов равно 3 – это исходы с номерами 2, 3, 5 Таблицы 1. Тогда
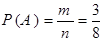 .
.
Пример. В коробке 6 белых шаров и 8 красных. Наудачу одновременно извлекаются 3 шара. Найти вероятность, того, что среди них будут:
а) два белых шара;
б) не менее одного белого.
Решение. а) Для удобства будем предполагать, что имеющиеся шары некоторым образом перенумерованы. Пусть, например, белые шары имеют номера 1, 2, …, 6 красные – 7, 8, …, 14. Тогда единичным исходом является произвольная тройка номеров: 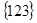 ,
, 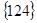 , …,
, …, 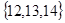 . (Оставляем читателю в качестве упражнения проверку того, что данные исходы удовлетворяют всем условиям классического определения вероятностей.)
. (Оставляем читателю в качестве упражнения проверку того, что данные исходы удовлетворяют всем условиям классического определения вероятностей.)
| Таблица 1. | |||
| Номер исхода | Номер монеты | ||
| О | О | О | |
| О | Р | О | |
| О | О | Р | |
| О | Р | Р | |
| Р | О | О | |
| Р | Р | О | |
| Р | О | Р | |
| Р | Р | Р |
Тогда общее число n исходов равно числу способов, которыми можно выбрать 3 номера из имеющихся 14-ти номеров. Напомним, что такое число равно соответствующему числу сочетаний:
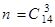 .
.
(В общем случае,
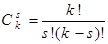
равно числу способов, которыми можно выбрать s объектов из k имеющихся объектов.) Таким образом,
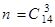 =
= 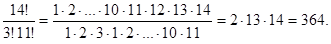
Найдем теперь число m исходов, благоприятствующих появлению двух белых шаров среди трех извлеченных. Число способов, которыми можно выбрать 2 шара из имеющихся 6-ти белых шаров, равно  . Но число благоприятствующих исходов с фиксированной парой белых шаров равно числу способов, которыми можно выбрать оставшийся красный шар в тройку, т.е. равно
. Но число благоприятствующих исходов с фиксированной парой белых шаров равно числу способов, которыми можно выбрать оставшийся красный шар в тройку, т.е. равно 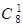 . Поэтому
. Поэтому
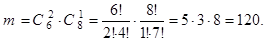
Окончательно имеем
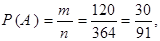
где А – событие состоящее в том, что среди трех отобранных шаров ровно 2 белых шара.
б) Полное число n исходов найдено в п. а). Число троек, в которых не менее 2-х белых шаров, равно сумме троек с двумя белыми шарами и троек с тремя белыми шарами:
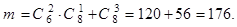
Окончательно имеем
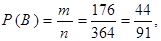

где В – событие состоящее в том, что среди трех отобранных шаров не менее 2-х белых шаров.