Формула полной вероятности. Формула Байеса (гипотез)

Теорема. Пусть события 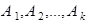образуют полную систему и F – некоторое событие. Тогда справедлива формула

,

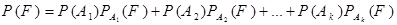которая и называется формулой полной вероятности.

Пусть событие F отлично от невозможного, тогда

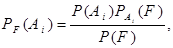
где 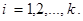Данная формула называется формулой Байеса (гипотез).

Пример. Объемы продукции, изготавливаемой двумя рабочими, относятся как 3: 2. Вероятности брака для деталей первого и второго рабочих равны соответственно 0, 02 и 0, 01. Найти вероятность того, что деталь, извлеченная наудачу из не рассортированной продукции,

а) является бракованной;

б) изготовлена первым рабочим, если известно, что она бракована.

Решение. а) Введем в рассмотрение события: 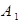– деталь изготовлена первым рабочим, 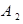– деталь изготовлена вторым рабочим, F – деталь бракована. Из условия следует, что всю продукцию можно предполагать состоящей из 5-ти частей (3+2=5), причем на долю первого рабочего приходится 3 части из этих 5-ти, на долю второго – 2 части. Тогда, по классическому определению вероятности, 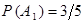, 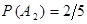. По условию,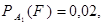 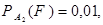и по формуле полной вероятности получаем

,

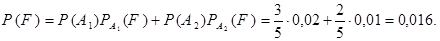б)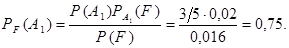

Домашнее задание: 1.72, 1.75.