Теорема сложения вероятностей.

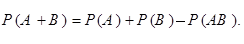
Важным частным случаем этой теоремы является

Теорема сложения вероятностей для несовместных событий. Вероятность суммы двух несовместных событий равна сумме их вероятностей, т.е.

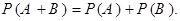
Доказательство. Так как события А и В несовместны, то их произведение равно невозможному событию, т.е. АВ = Æ. Поскольку вероятность невозможного события равна нулю (см. § 1.3), то из теоремы сложения вероятностей следует требуемое утверждение.

Отметим, что аналогичное утверждение справедливо для любого числа попарно несовместных событий: вероятность суммы попарно несовместных событий равна сумме их вероятностей.

Следствие. Пусть события 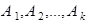образуют полную систему, тогда сумма их вероятностей равна 1 т.е.

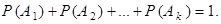
Доказательство. Из определения полной системы следует, что события 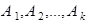, в частности, являются единственно возможными, поэтому 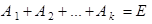(см. § 1.4). Тогда

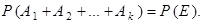
Вероятность достоверного события равна 1 (см. § 1.3). События 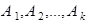, в частности, являются попарно несовместными. Тогда из теоремы сложения вероятностей для несовместных событий следует требуемое утверждение.

Данное следствие при 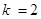представляет важное свойство противоположных событий: сумма вероятностей взаимно противоположных событий равна 1, т.е.

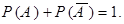
Определение. Условной вероятностью 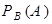называется вероятность наступления события А в предположении наступления события В.

Определение. Два события называются независимыми, если вероятность наступления одного из них не зависит от того, считается ли другое событие наступившим или нет.

Данное определение равносильно следующему:

события А и В независимы Û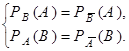

Пример. Пусть испытание состоит в извлечении карты из колоды. Событие А – извлечена “ картинка”, событие В – извлечена “7”. Выяснить, являются ли события А и В независимыми.

Решение. Так как среди “ картинок” нет “семерок”, то 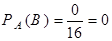. Так как среди “не картинок” – 4 “семерки”, то 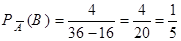. Таким образом,

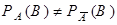, поэтому события А и В зависимы. Аналогично, в общем случае произвольные (неравные) несовместные события – зависимы.

Теорема ( необходимое и достаточное условие независимости событий ). События А и В независимы тогда и только тогда, когда

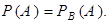
Пример. Пусть испытание состоит в бросании игральной кости, 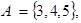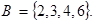Выяснить, являются ли события А и В независимыми.

Решение. Очевидно, что 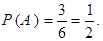В предположении обязательного наступления события В, полноечисло возможных исходов равно 4, из которых 2 исхода благоприятствуют наступлению события А, поэтому 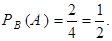Так как 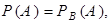то события А и В – независимы.