
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема умножения вероятностей.
|
|
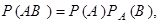
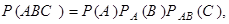
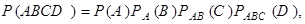 ………………………………………..
………………………………………..
|
Теорема умножения вероятностей для независимых событий. Вероятность произведения двух независимых событий равна произведению их вероятностей, т.е.
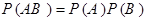 .
.
Аналогичное утверждение справедливо для любого числа независимых событий.
Пример. Два стрелка одновременно выстреливают в мишень. Вероятность попадания для первого стрелка равна 0, 6, для второго – 0, 8. Найти вероятность того, что в мишени будет:
а) одна пробоина;
б) хотя бы одна пробоина.
Решение. а) Прежде всего, укажем, когда может наступать интересующее нас событие, перебирая все возможные варианты.
В мишени будет одна пробоина
тогда и только тогда, когда
первый стрелок попал и второй стрелок промахнулся
или
первый стрелок промахнулся и второй стрелок попал.
Пусть событие А – в мишени будет одна пробоина, событие 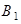 – первый стрелок попал, событие
– первый стрелок попал, событие 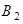 – второй стрелок попал. Тогда
– второй стрелок попал. Тогда 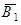 – первый стрелок промахнулся,
– первый стрелок промахнулся,
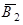 – второй стрелок промахнулся. “Тогда и только тогда, когда” соответствует отношению равенства событий. Соединительный союз “или” соответствует операции сложения событий. Соединительный союз “и” соответствует умножению событий. Тогда фраза русского языка, в которой мы перечислили все возможности для наступления события А, равносильна следующему символическому равенству
– второй стрелок промахнулся. “Тогда и только тогда, когда” соответствует отношению равенства событий. Соединительный союз “или” соответствует операции сложения событий. Соединительный союз “и” соответствует умножению событий. Тогда фраза русского языка, в которой мы перечислили все возможности для наступления события А, равносильна следующему символическому равенству
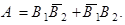
Откуда следует равенство вероятностей
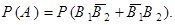
Так как события 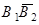 и
и 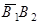 несовместны, то, применяя теорему сложения вероятностей для несовместных событий, приходим к равенству
несовместны, то, применяя теорему сложения вероятностей для несовместных событий, приходим к равенству
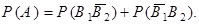
События 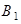 ,
, 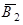 и
и 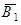 ,
, 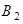 попарно независимы, поэтому, применяя теорему умножения вероятностей для независимых событий, получаем
попарно независимы, поэтому, применяя теорему умножения вероятностей для независимых событий, получаем
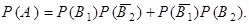
По условию, 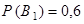 и
и 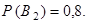 Тогда, по свойству взаимно противоположных событий (см. следствие из теоремы сложения вероятностей для несовместных событий,
Тогда, по свойству взаимно противоположных событий (см. следствие из теоремы сложения вероятностей для несовместных событий, 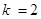 ),
), 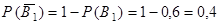 и
и 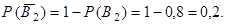 Окончательно имеем
Окончательно имеем
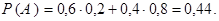
б) Пусть 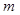 – число попаданий в мишень, тогда искомой является вероятность
– число попаданий в мишень, тогда искомой является вероятность 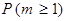 (заметим, что слова “хотя бы один”, “не менее чем один”, “по-крайней мере один” являются синонимами). Событие
(заметим, что слова “хотя бы один”, “не менее чем один”, “по-крайней мере один” являются синонимами). Событие 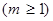 равносильно тому, что число попаданий в мишень будет равно 1 или 2, т.е.
равносильно тому, что число попаданий в мишень будет равно 1 или 2, т.е.
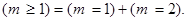
Тогда, учитывая несовместность событий 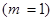 и
и 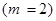 , получаем
, получаем
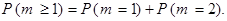
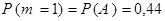 (см. п. а) данного примера). Событие
(см. п. а) данного примера). Событие 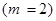 (два попадания в мишень) наступает тогда и только тогда, когда первый стрелок попадет в мишень и второй стрелок попадет, т.е.
(два попадания в мишень) наступает тогда и только тогда, когда первый стрелок попадет в мишень и второй стрелок попадет, т.е.
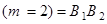 .
.
Поэтому
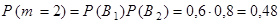
(см. теорему умножения вероятностей для независимых событий). Окончательно имеем

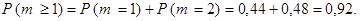
Отметим, что эта задача допускает и другое решение. Так как события 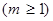 и
и 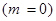 взаимно противоположны, то
взаимно противоположны, то
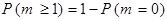 .
.
Но 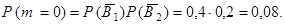 Следовательно
Следовательно
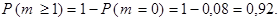
Пример. В коробке лежат4 белых шара и 6 красных. Наудачу, один за другим из коробки извлекается 2 шара. Найти вероятность того, что среди них будет:
а) один красный шар;
б) менее 2-х красных шаров.
Решение. а) Пусть событие А – среди двух извлеченных шаров – ровно один красный. Это событие наступает тогда и только тогда, когда первый из извлеченных шаров – красный, а второй – белый или первый шар – белый, а второй – красный. Напомним, что соединительный союз “или” соответствует сложению событий, союзы “и”, “а” соответствуют умножению событий. Тогда описание всех возможностей наступления события А равносильно следующему формальному равенству
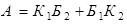 ,
,
где 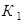 (
(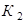 ) – первый (второй) шар – красный,
) – первый (второй) шар – красный, 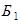 (
(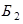 ) – первый (второй) шар – белый. События
) – первый (второй) шар – белый. События 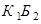 и
и 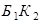 – несовместны, поэтому, используя теорему сложения вероятностей для несовместных событий, получаем
– несовместны, поэтому, используя теорему сложения вероятностей для несовместных событий, получаем

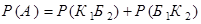 .
.
Применяя теперь теорему умножения вероятностей, приходим к равенству
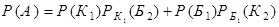 .
.
Для вычисления вероятностей из правой части последнего равенства используем классическое определение вероятности. Тогда

б) Пусть m – число красных шаров среди двух извлеченных. Тогда искомой является вероятность 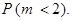 Очевидно, что
Очевидно, что 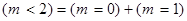 , и
, и  (см. п. а) данного примера). Вместе с тем, событие
(см. п. а) данного примера). Вместе с тем, событие 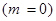 – среди извлеченных шаров нет красных – равносильно тому, что первый шар окажется белым и второй – также белым, т.е.
– среди извлеченных шаров нет красных – равносильно тому, что первый шар окажется белым и второй – также белым, т.е. 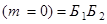 , поэтому
, поэтому
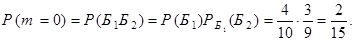
Окончательно имеем
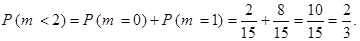
Заметим, что вероятность 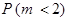 может быть также найдена по-другому. События
может быть также найдена по-другому. События 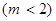 и
и 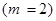 взаимно противоположны, поэтому
взаимно противоположны, поэтому
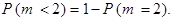
Но
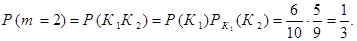
Тогда
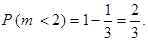
Домашнее задание (здесь и далее номера задач указаны по учебнику Н.Ш. Кремера “Теория вероятностей и математическая статистика”): 1.54, 1.58, 1.60, 1.61, 1.64, 1.69.