Закон распределения дискретной случайной величины

Определение. Случайной величиной называется переменная, которая в результате испытания принимает то или иное числовое значение.

Пример. Число попаданий в мишень при 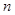выстрелах – случайная величина.

Пример. Рост наудачу взятого человека – случайная величина.

Определение. Случайная величина называется дискретной, если число ее возможных значений конечно или счетно.

(Напомним, что множество называется счетным, если его элементы можно перенумеровать натуральными числами.)

В этом смысле, число попаданий в мишень – пример дискретной случайной величины. Рост человека – непрерывная случайная величина (такие случайные величины будут рассмотрены ниже).

Для обозначения случайных величин будем использовать заглавные буквы латинского алфавита (возможно с индексами), например, 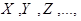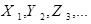и т.п.

Определение. Законом распределения дискретнойслучайной величины называется такая таблица, в которой перечислены все возможные значения этой случайной величины (без повторений) с соответствующими им вероятностями.

В общем виде закон распределения для случайной величины, например, :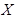

:				…
			…

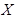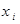
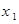
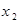
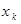
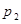
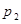
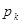
где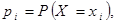

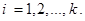
Из определения закона распределения следует, что события 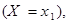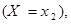…, 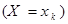образуют полную систему, поэтому (см. следствие из теоремы сложения вероятностей для несовместных событий в §1.6):

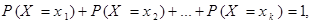
т.е.

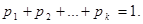
Данное равенство называется основным свойством закона распределения.

Пример. Два стрелка одновременно выстреливают в мишень. Вероятность попадания для первого равна 0, 6, для второго – 0, 8. Составить закон распределения случайной величины 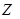– общего числа попаданий в мишень.

Решение. Возможные значения данной случайной величины: 0, 1, 2. Так же как в примере из §1.6, через 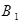и 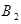обозначим события, состоящие в попадании в мишень первого и второго стрелков (соответственно). Тогда аналогично упомянутому примеру получаем

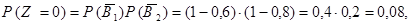
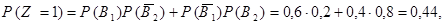
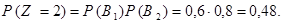
Окончательно, закон распределения случайной величины 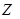имеет вид:

:
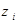
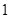
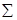
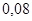
		0, 44	0, 48

Упражнение. В коробке 3 белых шара и 2 красных. Составить закон распределения случайной величины 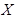– числа белых шаров среди 2-х извлеченных шаров.

Ответ.

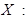
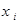
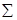
	0, 1	0, 6	0, 3

Пример. В коробке – 3 белых шара и 2 красных. Шары извлекаются последовательно до появления белого шара. Составить закон распределения случайной величины Х – числа извлеченных шаров.

Решение. Возможные значения данной случайной величины: 1, 2, 3. Событие 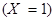(из коробки будет извлечен один единственный шар) наступает тогда и только тогда, когда первый из шаров оказывается белым, т.к. появление именно белого шара является сигналом к прекращению последующих извлечений (см. условие). Поэтому

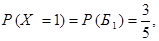
где событие 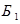– первый из извлеченных шаров – белый. Событие 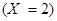(из коробки будет извлечено ровно 2 шара) наступает тогда и только тогда, когда первый из извлеченных шаров оказывается красным, а второй – белым. Поэтому

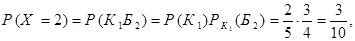
где событие 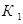– первый из извлеченных шаров – красный, 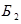– второй шар – белый. Наконец событие 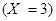(из коробки будет извлечено 3 шара) наступает тогда и только тогда, когда первый шар – красный, второй – красный и третий – белый. Поэтому

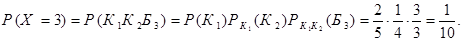
Окончательно искомый закон распределения имеет вид:

Х: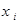
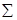
	0, 6	0, 3	0, 1

Упражнение. Имея 3 патрона, стрелок стреляет по мишени до первого попадания (или до израсходования патронов). Вероятность попадания при каждом выстреле равна 0, 8. Составить закон распределения случайной величины Х – числа произведенных выстрелов.

Ответ.

Х: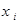
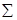
	0, 8	0, 16	0, 04

Пример. Стрелок стреляет в мишень 3 раза. Вероятность попадания при каждом выстреле равна 0, 8. Составить закон распределения случайной величины Х – числа попаданий в мишень.

Решение. Возможные значения для числа попаданий: 0, 1, 2, 3. Вероятности того, что случайная величина Х примет эти значения вычисляются по формуле Бернулли при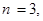

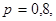
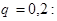
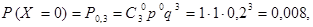
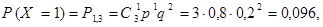
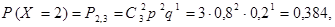
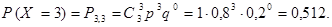
Окончательно искомый закон распределения имеет вид:

Х: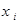
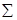
	0, 008	0, 096	0, 384	0, 512

Полученный закон распределения является частным случаем так называемого биномиального закона распределения (при ).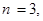

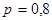Определение. Случайная величина Х имеет биномиальный закон распределения с параметрам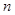и и 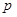, если ее закон распределения имеет вид:

Х:					…		,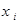
				…

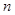
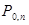
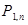
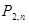
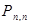
где вероятности 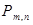вычисляются по формуле Бернулли:

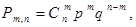
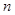– положительное целое число,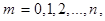

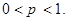
В пределе пр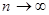и и 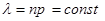биномиальное распределение переходит в так называемое распределение Пуассона.

Определение. Говорят, что случайная величина Х имеет распределение Пуассона с параметром 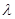, если ее закон распределения имеет вид:

Х:					…	,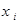
				…

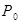
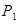
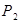
где

,

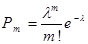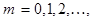
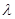– положительное число.

Убедимся в том, что для распределения Пуассона выполняется основное свойство закона распределения: 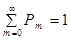. Действительно, имеем

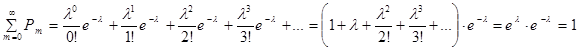
(см. курс математического анализа, разложение функции 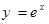в ряд Маклорена).

Домашнее задание. 3.25, 3.31, 3.36, 3.40, 3.45.