Параметры распределения дискретной случайной величины

Пусть закон распределения дискретной случайной величины Х имеет вид

:				…
			…

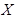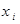
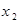
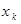
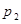
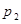
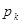
Определение. Математическим ожиданием дискретной случайной величины Х называется число М(Х), вычисляемое по формуле

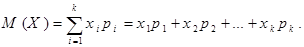
Математическое ожидание случайной величиныесть число около которого группируются значения этой случайной величины.

Механическим аналогом математического ожидания дискретной случайной величины является центр масс (центр тяжести) системы точечных масс: если в точках числовой оси с абсциссами 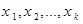расположены точечные массы 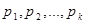, то абсцисса их центра масс находится точно по формуле для 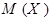, приведенной выше.

Пример. Пусть случайная величина Х биномиально распределена с параметрам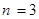и и 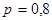(см. пример из § 3.1):

Х: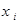
	0, 008	0, 096	0, 384	0, 512

Тогда