Неравенство Чебышёва

Лемма Чебышёва. Пусть среди значений случайной величины 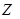нет отрицательных. Тогда вероятность того, что в некотором испытании значение этой случайной величины превысит число 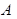, оценивается по формуле

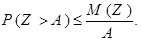
Так как события 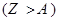и 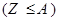взаимно противоположны, то 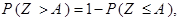и лемма Чебышёва может быть также представлена в виде

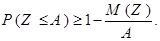
Пример. В среднем в течение часа на вокзал прибывает 400 пассажиров. Оценить:

а) вероятность того, что число пассажиров, прибывших на вокзал в течение часа, будет более 420;

б) верхнюю границу для числа прибывших пассажиров, которую можно гарантировать с вероятностью не меньшей 0, 9.

Решение. Пусть 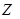– число пассажиров, прибывающих на вокзал в течение наудачу выбранного часа. По условию, значения этой случайной величины группируются около 400. Тем самым, имеем 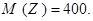Полагая в неравенстве Чебышёва 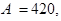получаем

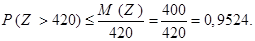
Из условия и второй формы записи неравенства Чебышёва следует, что

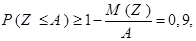
где 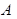– искомая верхняя граница для числа пассажиров. Таким образом, имеем равенство

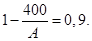
Решая это уравнение относительно 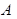, получаем: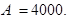

Неравенство Чебышёва. Для произвольной случайной величины 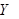вероятность того, что в некотором испытании значение этой случайной величины будет отличаться от математического ожидания 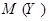не более чем на 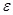(по абсолютной величине), оценивается по формуле

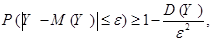
где 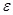– произвольное положительное число.

Рассмотрим следствия из неравенства Чебышёва.

Следствие 1. Пусть случайные величины 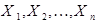– независимы, 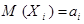, 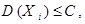где 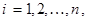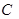– некоторое число. Тогда вероятность того, что среднее арифметическое этих случайных величин отличается от среднего арифметического их математических ожиданий не более чем на 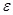(по абсолютной величине), оценивается по формуле

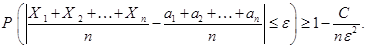
Следствие 2. Пусть случайные величины 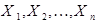– независимы, 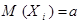, 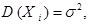где 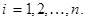Тогда вероятность того, что среднее арифметическое этих случайных величин отличается от их общего математического ожидания не более чем на 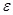(по абсолютной величине), оценивается по формуле

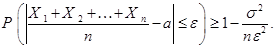
Следствие 3. Пусть 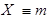– число наступлений некоторого события 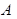в 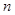повторных независимых испытаниях, в каждом из которых это событие наступает с вероятностью 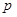. Тогда вероятность того, что число 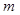наступлений события 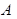отличается от 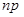не более чем на 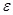(по абсолютной величине), оценивается по формуле

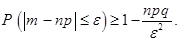
Следствие 4. Пусть 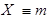– число наступлений некоторого события 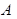в 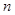повторных независимых испытаниях, в каждом из которых это событие наступает с вероятностью 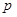. Тогда вероятность того, что частость 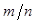наступлений события 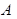отличается от вероятности 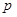не более чем на 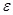(по абсолютной величине), оценивается по формуле

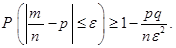
Последнее следствие называется также неравенством Бернулли.

Пример. Вероятность сделать покупку для каждого из покупателей магазина равна 0, 7. Почему нельзя применить неравенство Чебышёва для оценки вероятности того, что из 1000 покупателей доля таких, которые приобретут в магазине товар, будет заключена в границах от 0, 67 до 0, 72? Как следует изменить левую границу, чтобы применение неравенства Чебышёва стало возможным? Решить задачу при соответствующем изменении левой границы. Найти эту же вероятность по интегральной теореме Муавра-Лапласа. Объяснить различие в полученных результатах. Сколько покупателей надо обследовать, чтобы те же границы для рассматриваемой доли можно было гарантировать с вероятностью не меньшей 0, 9?

Решение. Неравенство Чебышёва позволяет оценивать вероятности попадания значения случайной величины только в границы, которые симметричны относительно математического ожидания этой случайной величины. Но в данном случае интервал (0, 67; 0, 72) несимметричен относительно 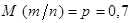, где 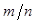– доля покупателей, которые приобретут в магазине товар, 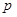– вероятность приобретения товара. Соответственно, для того, чтобы применение неравенства Чебышёва стало возможным, левая граница интервала должна отстоять от 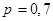ровно настолько, насколько отстоит правая, т.е. на 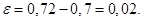Неравенства 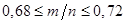и 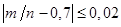– равносильны, а вероятность 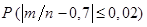оценивается по следствию 4 (неравенству Бернулли) при , , :

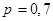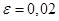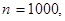
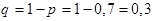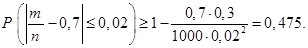
Точно такая же вероятность может быть найдена по следствию 2 из интегральной теореме Муавра-Лапласа:

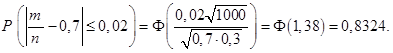
Очевидно, что полученные результаты не противоречат друг другу. Поясним, почему для одной и той же вероятности неравенство Чебышёва дает лишь оценку, в то время как теорема Муавра-Лапласа – точное значение. Дело в том, что неравенство Чебышёва получено без каких бы то ни было предположений о законе распределения рассматриваемой случайной величины. В результате область его применений широка, но получение точных результатов с его помощью оказывается невозможным. В свою очередь, теорема Муавра-Лапласа опирается на свойство биномиального распределения: по центральной предельной теореме, это распределение неограниченно приближается к нормальному при неограниченном увеличении числа испытаний. Использование закона распределения рассматриваемой случайной величины и позволяет уточнить окончательный результат.

Перейдем теперь к последнему заданию данной задачи. По условию и неравенству Бернулли, имеем

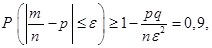
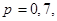
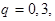
причем 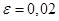. Тогда полученное равенство

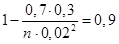
содержит единственную неизвестную: 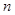. Решая это уравнение относительно этой неизвестной, получаем: