Коэффициент корреляции и его свойства

Определение. Коэффициентом корреляции 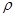случайных величин Х и Y называется число, определяемое равенством

где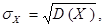

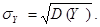
Коэффициент корреляции является мерой тесноты линейной связи между переменными.

Величина 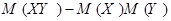называется ковариацией и обозначается .

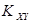Замечание. Из свойства математического ожидания (см. § 3.3) следует, что, если случайные величины Х и Y независимы, то коэффициент корреляции 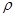равен нулю. Существенно, что обратное утверждение неверно, т.е. в общем случае из условия равенства коэффициента корреляции нулю не следует, что данные случайные величины независимы.

Упражнение. Совместное распределение случайных величин X и Y имеет вид:

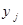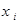
	0, 2	0, 2
	0, 3	0, 3

Убедиться, что 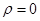и данные случайные величины независимы.

Упражнение. По совместному распределению Примера # вычислить коэффициент корреляции. (Ответ. )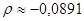

Упражнение. Совместное распределение величин X и Y имеет вид:

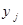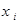
-1	0, 2
		0, 6
	0, 2

Убедиться, что 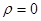, но данные случайные величины – зависимы (более того, можно заметить, что в данном случае X и Y связаны наиболее “жесткой” из всех возможных связей – функциональной: ).

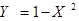Теорема (Область возможных значений коэффициента корреляции). Модуль коэффициента корреляции не превосходит1, т.е.

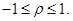
Теорема. Если модуль коэффициента корреляции двух случайных величин равен 1, то между этими случайными величинами существует линейная функциональная зависимость.

Пример. Пусть совместный закон распределения случайных величин X и Y имеет вид:

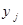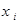
	0, 4
		0, 6

Тогда 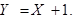Оставляем читателю в качестве упражнения проверку того, что в данном случае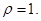

Из определения ковариации следует, что

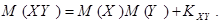
Другими словами, ковариация является мерой неравенства между математическим ожиданием произведения двух случайных величин и произведением их математических ожиданий. Аналогично, применительно к дисперсии, справедливо равенство