Оценка неизвестного параметра. Свойства оценок

Определение. Случайная величина 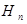называется оценкой неизвестного параметра 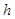, если значение этой случайной величины, найденное по результатам серии из 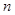измерений, может быть принято за приближенное значение этого параметра т.е. если справедливо равенство .

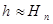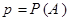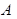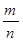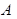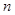Пример. Если в качестве неизвестного параметра рассматривается вероятность наступления некоторого события , то оценкой этого параметра служит частость наступлений события в независимых испытаниях (см. статистическое определение вероятности и теорему Бернулли).

Пример. Пусть случайные величины 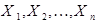имеют одинаковое математическое ожидание, т.е. 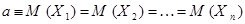. Тогда оценкой значения 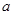общего математического ожидания таких случайных величин служит среднее арифметическое 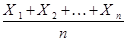этих случайных величин. Важным частным случаем рассмотренной ситуации является следующий

Пример. Оценкой некоторого параметра 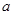служит среднее арифметическое 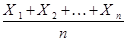результатов 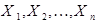независимых измерений этого параметра (см. теорему Чебышёва).

При непосредственном использовании приближенного равенства 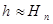говорят о точечном оценивании неизвестного параметра.

Возможно также интервальное оценивание неизвестного параметра. Для того, чтобы объяснить, в чем оно состоит, введем в рассмотрение следующие понятия.

Определение. Для произвольного 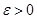интервал 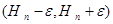называется доверительным интервалом; сама величина 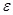называется в этом случае предельной ошибкой выборки.

Определение. Вероятность того, что неизвестное значение оцениваемого параметра накрывается доверительным интервалом, называется доверительной вероятностью.

Таким образом, если 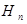– оценкапараметра 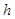, то

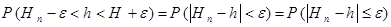
– доверительная вероятность (мы предполагаем, что оценка 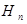является непрерывной случайной величиной).

Интервальное оценивание состоит, например, в вычислении доверительной вероятности для заданной предельной ошибки выборки.

Решение задачи интервального оценивания связано с определением характера закона распределения используемой оценки .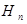

Рассмотрим теперь некоторые свойства оценок.

Определение. Оценка 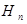параметра 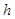называется несмещенной, если математическое ожидание этой оценки равно оцениваемому параметру, т.е.

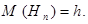
Определение. Оценка 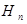параметра 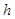называется состоятельной, если для произвольного 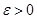выполняется следующее предельное соотношение

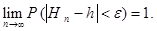
Другими словами, оценка 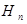параметра 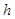состоятельна, если эта оценка сходится по вероятности к данному параметру. (Напомним, что примеры сходимости такого рода дают теоремы Бернулли и Чебышёва, см. § 6.2.)

Определение. Несмещенная оценка некоторого параметра называется эффективной, если она обладает наименьшей дисперсией среди всех несмещенных оценок, найденных по выборке заданного объема.

Пример. Частость 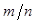наступления некоторого события является несмещенной, состоятельной и эффективной оценкой вероятности 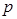этого события. Заметим, что свойства несмещенности и состоятельности частости были фактически рассмотрены нами ранее в несколько ином контексте. Действительно, несмещенность частости – равенство 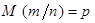– является одним из свойств биномиально распределенной случайной величины (см. § 3.3). Состоятельность частости утверждается теоремой Бернулли (см. § 6.2).

Пример. Среднее арифметическое некоторого числа независимых и одинаково распределенных случайных величин является несмещенной и состоятельной оценкой общего математического ожидания этих случайных величин. Действительно, несмещенность – есть свойство 5 математического ожидания (см. § 3.3). Состоятельность утверждается теоремой Чебышёва (см. § 6.2).