
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка генеральной средней
|
|
Пусть задана генеральная совокупность объектов, для которой фиксирован некоторой числовой признак 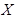 . Требуется оценить среднее значение признака
. Требуется оценить среднее значение признака 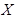 в генеральной совокупности – генеральную среднюю
в генеральной совокупности – генеральную среднюю 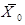 . Для этого из генеральной совокупности выделяют часть (выборку), и по результатам ее обследования находят среднее значение признака
. Для этого из генеральной совокупности выделяют часть (выборку), и по результатам ее обследования находят среднее значение признака 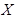 в выборке – выборочную среднюю
в выборке – выборочную среднюю 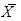 , с помощью которой и выполняют оценивание неизвестного значения
, с помощью которой и выполняют оценивание неизвестного значения 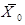 . Другими словами, выборочная средняя
. Другими словами, выборочная средняя 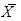 является оценкой генерального среднего
является оценкой генерального среднего 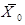 .
.
Пример. Пусть некоторая совокупность деталей обследуется на предмет их длины. Тогда 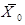 – средняя длина деталей в генеральной совокупности,
– средняя длина деталей в генеральной совокупности, 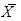 – средняя длина деталей в выборке,
– средняя длина деталей в выборке, 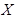 – длина детали, взятой наудачу из генеральной совокупности.
– длина детали, взятой наудачу из генеральной совокупности.
В том случае, когда оценивание сводится к использованию приближенного равенства 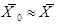 , говорят о точечном оценивании генеральной средней (см. § 7.1).
, говорят о точечном оценивании генеральной средней (см. § 7.1).
Возможно также интервальное оценивание генеральной средней (см. § 7.1). Для того чтобы объяснить, в чем оно состоит, введем в рассмотрение следующие понятия.
Определение. Для произвольного 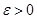 интервал
интервал 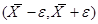 называется доверительным интервалом; величина
называется доверительным интервалом; величина 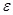 называется в этом случае предельной ошибкой выборки.
называется в этом случае предельной ошибкой выборки.
Определение. Вероятность того, что неизвестное значение генеральной средней 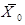 накрывается доверительным интервалом, называется доверительной вероятностью.
накрывается доверительным интервалом, называется доверительной вероятностью.
Таким образом,
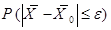
– доверительная вероятность.
Интервальное оценивание состоит, например, в вычислении доверительной вероятности для заданной предельной ошибке выборки.
Как и всякая оценка, выборочная средняя 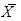 является случайной величиной. Действительно, элементы выборки отбираются из генеральной совокупности случайным образом, а значение
является случайной величиной. Действительно, элементы выборки отбираются из генеральной совокупности случайным образом, а значение 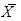 зависит от того, какие именно элементы попали в выборку. Рассмотрим свойства выборочной средней
зависит от того, какие именно элементы попали в выборку. Рассмотрим свойства выборочной средней 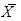 как случайной величины.
как случайной величины.
Теорема 1. Математическое ожидание выборочной средней 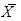 равно генеральной средней
равно генеральной средней 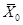 , то есть
, то есть
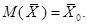
Среднее квадратическое отклонение 
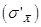 выборочной средней вычисляется по формулам
выборочной средней вычисляется по формулам
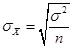
– в случае повторной выборки и
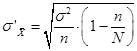
– в случае бесповторной,
где 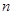 – объем выборки,
– объем выборки, 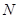 – объем генеральной совокупности,
– объем генеральной совокупности, 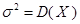 – дисперсия признака
– дисперсия признака 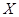 для рассматриваемой генеральной совокупности (генеральная дисперсия).
для рассматриваемой генеральной совокупности (генеральная дисперсия).
Напомним, что, по определению среднего квадратического отклонения,  равно корню квадратному из дисперсии выборочной средней, то есть
равно корню квадратному из дисперсии выборочной средней, то есть

(аналогично в случае бесповторной выборки).
Замечание. При применении на практике формул Теоремы 1 полагают, что
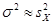 .
.
Теорема 2. Закон распределения выборочной средней неограниченно приближается к нормальному при неограниченном увеличении объёма выборки.
Согласно результатам § 4.3, для произвольной нормально распределенной случайной величины 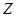 справедлива формула
справедлива формула
 .
.
Учитывая Теорему 2, в последнем равенстве положим 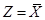 . Тогда, по Теореме 1,
. Тогда, по Теореме 1, 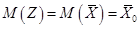 и
и 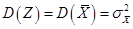 , и приведенная формула – свойство нормального закона распределения принимает вид:
, и приведенная формула – свойство нормального закона распределения принимает вид:
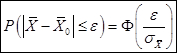 .
.
Вероятность, стоящая в левой части последнего равенства называется доверительной вероятностью (см. выше), поэтому сама эта формула называется формулой доверительной вероятности.
Теорема 3. Выборочная средняя 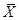 является несмещенной и состоятельной оценкой генеральной средней
является несмещенной и состоятельной оценкой генеральной средней 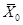 .
.
Пример. Для обследования средней заработной платы трехсот рабочих была образована выборка, состоящая из пятидесяти рабочих. Результаты выборочного обследования представлены в таблице:
| Заработная плата в месяц, ден. ед. | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 | 200-220 | 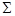
|
| Число рабочих |
1. Найти вероятность того, что средняя заработная плата всех рабочих отличается от средней выборочной не более чем на 5 ден. ед. (по абсолютной величине) в случае повторной и бесповторной выборок.
2. Найти границы, в которых с вероятностью 0, 9545 заключена средняя заработная плата всех рабочих.
3. Сколько рабочих надо взять в выборку, чтобы полученные в п. 2 доверительные границы можно было гарантировать с вероятностью 0, 9973.
Решение. Исходный вариационный ряд является интервальным. Для нахождения его характеристик, прежде всего, сведем этот вариационный ряд к дискретному:
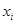
| 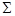
| ||||||
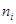
|
где 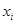 – возможное значение заработной платы – середина
– возможное значение заработной платы – середина 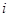 - го интервала исходного вариационного ряда (ден. ед.);
- го интервала исходного вариационного ряда (ден. ед.); 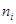 – число рабочих;
– число рабочих; 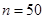 .
.
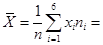
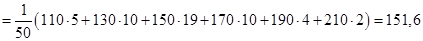 .
.
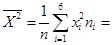
 .
.
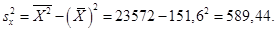
Для нахождения доверительной вероятности (см. п. 1 задания) воспользуемся одноименной формулой при 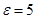 . Но сначала вычислим средние квадратические отклонения выборочной средней для каждого из рассматриваемых типов выборок.
. Но сначала вычислим средние квадратические отклонения выборочной средней для каждого из рассматриваемых типов выборок.
а) Повторная выборка.
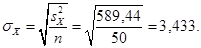
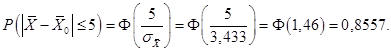
б) Бесповторная выборка, 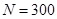 .
.
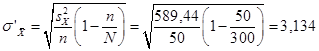 .
.
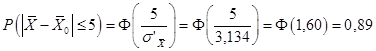 .
.
Доверительный интервал в данном случае: 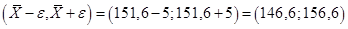 .
.
Тем самым получаем, что: неизвестное значение средней заработной платы всех рабочих накрывается интервалом (146, 6; 156, 6) с вероятностью 0, 8557 в случае повторной выборки и с вероятностью 0, 89 в случае бесповторной выборки.
В п. 2 задания искомым является доверительный интервал, для нахождения которого следует вычислить предельную ошибку выборки 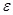 . Из условия и формулы доверительной вероятности в случае повторной выборки следует, что
. Из условия и формулы доверительной вероятности в случае повторной выборки следует, что
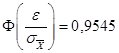 .
.
По таблице значений функции Лапласа найдем такое значение 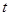 , что
, что 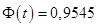 . Имеем
. Имеем 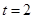 . Поскольку
. Поскольку
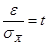 ,
,
то
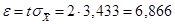 .
.
Соответствующий доверительный интервал:
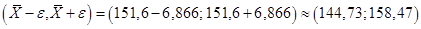 .
.
Аналогично, в случае бесповторной выборки имеем
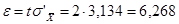 .
.
Соответствующий доверительный интервал:
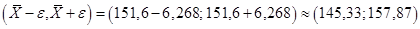 .
.
Таким образом, неизвестное значение средней заработной платы всех рабочих с вероятностью 0, 9545 накрывается доверительным интервалом (144, 73; 158, 47) в случае повторной выборки и доверительным интервалом (145, 33; 157, 87) в случае бесповторной выборки.
При решении п. 3 задания будем считать известными приближенные значения выборочной средней 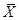 и выборочной дисперсии
и выборочной дисперсии 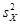 . Также используем предельные ошибки выборки
. Также используем предельные ошибки выборки 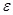 , найденные в п. 2. Рассмотрим сначала случай повторной выборки.
, найденные в п. 2. Рассмотрим сначала случай повторной выборки.
Из условия и формулы доверительной вероятности следует, что
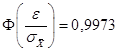 .
.
По таблице значений функции Лапласа найдем такое значение аргумента 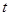 , что
, что 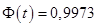 :
:  . Тогда
. Тогда
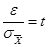 и
и 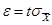 .
.
Используя известную формулу для 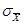 (см. Теорему 2 данного параграфа), имеем равенство:
(см. Теорему 2 данного параграфа), имеем равенство:
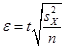 ,
,
в котором единственной неизвестной является искомый объем выборки 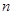 . Решая получившееся уравнение относительно
. Решая получившееся уравнение относительно 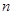 , получаем
, получаем
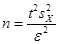 .
.
Подставляя в правую часть последнего равенства известные величины, получаем
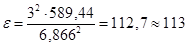
(заметим, что округление в данном случае, по смыслу искомой величины, следует произвести до целых, причем в большую сторону, чтобы обеспечить, как говорят, запас по вероятности).
Повторяя проведенные рассуждения для случая бесповторной выборки, имеем:
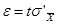 ,
,
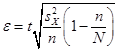 .
.
Решая полученное уравнение относительно 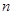 , получаем
, получаем
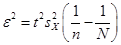 ,
,
откуда
 ,
,
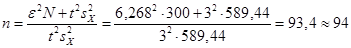
(также как и выше округление здесь произведено в большую сторону).
Таким образом, для того, чтобы с вероятностью 0, 9973 неизвестное значение средней заработной платы всех рабочих накрывалось доверительным интервалом (144, 73; 158, 47) в случае повторной выборки, в эту выборку следует взять 113 рабочих. Аналогично, для того, чтобы с вероятностью 0, 9973 неизвестное значение средней заработной платы всех рабочих накрывалось доверительным интервалом (145, 33; 157, 87) в случае бесповторной выборки, в выборку следует взять 94 рабочих.
Замечание. Если в задаче на выборочный метод объем генеральной совокупности много больше объема выборки (в ряде случаев это предполагается по умолчанию, а объем генеральной совокупности просто не указан), естественно считать, что 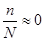 . Как следует из формул Теоремы 1, случаи повторной и бесповторной выборок дают тогда совпадающие результаты.
. Как следует из формул Теоремы 1, случаи повторной и бесповторной выборок дают тогда совпадающие результаты.