Элементарные операции с матрицами

Две матрицы считаются равными тогда и только тогда, когда они имеют одинаковые размерности и соответствующие элементы,

.

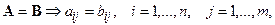Сложение двух матриц A и B:

C = A + B 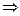с_ij = a_ij + b_ij, i =1,..., n, j =1,..., m, dim A =dim B=dim С.

Операция сложения матриц обладает переместительным и сочетательным свойствами:

А + В = В + А;

(А + В) + С = А + (В + С).

Здесь А, В, С произвольные прямоугольные матрицы одинакового размера.

Умножение матрицы на число: B = a A, 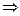b_ij = aa_ij, i =1,..., n, j=1,..., m
(dim A =dim B). Для данной операции справедливы следующие свойства:

a( A + B ) = a A + a B;

(a + b) A = a A +b A

(ab) A = a(b A )

Произведение двух матриц А и В:

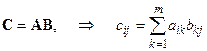i =1,..., n, j =1,..., s, dim A =n, m, dim B =m, s, dim C =n, s.

Эта операция возможна при условии, что количество столбцов матрицы A равно количеству строк матрицы В. Матрица - произведение С имеет столько же столбцов, сколько их у матрицы B, и столько же строк, сколько их у матрицы A. Элемент с_ij - есть скалярное произведение i - той строки матрицы А и j - ого столбца матрицы B: с_ij. = .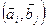

Для умножения матриц справедливо сочетательное свойство, а также распределительное свойство умножения относительно сложения:

(АВ) С = А (ВС);

(А + В) С = АС + ВС;

А (В + С) = АВ + АС.

Умножение матриц не обладает переместительным свойством: АВ ¹ ВА

(Если АВ = ВА, то матрицы А и В называются перестановочными или коммутирующими между собой).