Понятие о матрицах и матричных операциях

В данном разделе кратко приводятся основные понятия о матрицах, их характеристиках и свойствах. Предполагается, что читатель уже имел с ними дело в курсе высшей математики.

Матрица А порядка (n, m) - это прямоугольная таблица чисел или других элементов { a_ij }, расположенных в n строках и m столбцах.

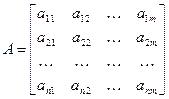
Числа n, m определяют размерность (dim A) матрицы.

Как правило, для обозначения матриц используются прописные буквы латинского алфавита, с возможным указанием размерности: А; B _{n, m;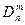} . При необходимости элементного обозначения используются скобки: квадратные (см. выше), круглые, двойные прямые. Кроме того, используются индексные элементные обозначения, например матрица || a_ij ||, i=1,..., n; j=1,..., m или (a_ij, i=1,..., n, j=1,..., m).

Транспонированная матрица А^t получается из исходной А заменой местами строк и столбцов (строка i матрицы А^t совпадает со столбцом i матрицы А)

Частные случаи:

Матрица-строка [z₁, z₂,..., z_n]; матрица-столбец (х₁, х₂,..., х_n)^t; квадратная матрицаn=m; симметричнаяматрица А = А^t ; кососимметричная матрица А = - А^t , диагональная матрица – такая, у которой все недиагональные элементы равны нулю; единичная матрицаЕ - это диагональная матрица, у которой все диагональные элементы равны единице; ортогональнаяматрица А^t=А^-1, нулевая матрица – матрица, у которой все элементы равны нулю.

Нижняя и верхняя треугольные матрицы характеризуются тем, что у них все элементы соответственно над или под главной диагональю равны нулю, например,

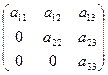и .

Блочная матрица – матрица, элементы которой являются также матрицами, например,

.
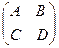
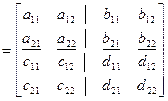