Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные пространства.
|
|
Основные понятия многомерных нормированных линейных пространств определены в курсе математического анализа, поэтому в данной главе дано лишь краткое изложение результатов, которые будут использоваться в задачах решения СЛУ итерационными методами и при анализе методов решения систем нелинейных и дифференциальных уравнений.
Основные понятия и определения
Пространство - совокупность конечного или бесконечного числа элементов, связанных общностью свойств, структуры, функций и др.
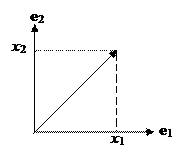 Вектор. Элементы пространства называются векторами. Обычно под вектором мы понимает некоторый направленный отрезок. Здесь понятие вектора шире, но не противоречиво. Вектор произвольного пространства можно представить в виде направленной структуры. В частности, вектор- столбец чисел размерности n может быть представлен в виде направленного отрезка, координатами которого (проекциями на оси) являются числа столбца. Например, на рис. 7.1 представлен вектор
Вектор. Элементы пространства называются векторами. Обычно под вектором мы понимает некоторый направленный отрезок. Здесь понятие вектора шире, но не противоречиво. Вектор произвольного пространства можно представить в виде направленной структуры. В частности, вектор- столбец чисел размерности n может быть представлен в виде направленного отрезка, координатами которого (проекциями на оси) являются числа столбца. Например, на рис. 7.1 представлен вектор 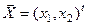 . Вектора, как правило, представляются либо буквами со стрелкой сверху, либо полужирным шрифтом.
. Вектора, как правило, представляются либо буквами со стрелкой сверху, либо полужирным шрифтом.
| Рис. 7.1. Вектор |
|
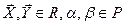 , то
, то 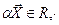
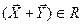 ) и при наличии следующих свойств операций:
) и при наличии следующих свойств операций:
Коммутативность операций сложения и умножения на число: ` 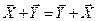 ; a
; a  =`
=`  a,
a,
Дистрибутивность: 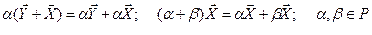
Ассоциативность: 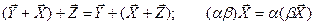
Наличие общего элемента – нуля – Q: 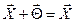
Свойство умножения на единичный коэффициент, если a = 1, то a  =
= 
Если P – поле вещественных чисел, то пространство называется вещественным векторным пространством. Если же Р – поле комплексных чисел, то R называется комплексным линейным пространством.
Примеры:
· В3 - множество всех векторов в трехмерном пространстве;
· Rn - упорядоченная совокупность n вещественных чисел (n-мерный вектор);
· множество C [ a, b ] – всех функции f(t), определенной на [ a, b ];
· множество Pn(t) всех алгебраических многочленов степени n;
· множество положительных вещественных чисел (здесь сумма векторов X+Y эквивалентна произведению чисел, а операция умножения вектора X на число λ эквивалентна возведению в степень λ).