Ингибирование

Ингибирование это уменьшение скорости реакции под действием определенных веществ – ингибиторов. По механизму ингибирования различают: обратимое и необратимое ингибирование. Обратимое ингибирование бывает:

· конкурентное ингибирование – ингибитор конкурирует с субстратом за активный центр, так как имеет схожее строение с субстратом и образует неактивный комплекс фермент-ингибитор;

· неконкурентное ингибирование – ингибитор не конкурирует с субстратом за активный центр, так как присоединяется к другой части фермента с образованием неактивных комплексов фермент-ингибитор и фермент-субстрат-ингибитор;

· бесконкурентное ингибирование – ингибитор не конкурирует с субстратом за активный центр, так как присоединяется к другой части фермента с образованием неактивных комплексов только фермент-субстрат-ингибитор.

Конкурентное ингибирование:

k₁ k₂

S +E ↔ ES → P

k_-1

E+I ↔ EI

Константа ингибирования K_I (константа диссоциации комплекса фермент-ингибитор) определяется выражением (принцип квазиравновесных концентраций):

Скорость реакции определяется скоростью медленной стадии:

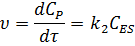
Скорость образования промежуточного вещества:

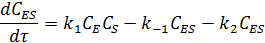
При условиях:

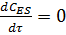· (концентрация фермент-субстратного комплекса стационарна);

· ;

· ;

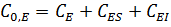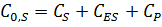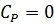· (в начальный момент времени отсутствует продукт);

· (начальная концентрация субстрата значительно выше начальной концентрации фермента) это означает, что мало и .

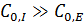· (начальная концентрация ингибитора значительно выше начальной концентрации фермента) это означает, что .

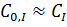Используя константу ингибирования:

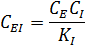
для начальной концентрации фермента можно записать:

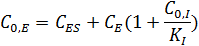
Концентрацию фермент-субстратного комплекса можно выразить уравнением:

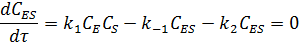
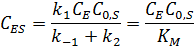
Отсюда, концентрация фермента равна:

Подставляя полученное уравнение в выражение для начальной концентрации фермента и решая его относительно концентрации фермент-субстратного комплекса, можно получить:

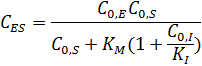
Начальная скорость реакции в присутствии ингибитора всегда меньше скорости реакции в его отсутствие (слагаемое 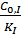в знаменатиле), а максимальные значения скоростей адинаковы:

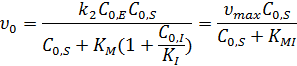
где 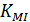– константа, зависящая как от начальной концентрации ингибитора, так и от константы ингибирования:

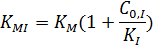
Константа ингибирования:

Таким образом, для определения константы ингибирования необходимо знать значения двух констант.

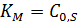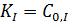Если , а то:

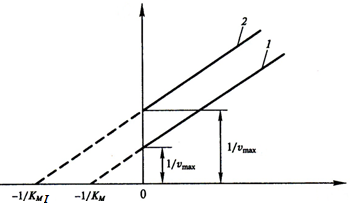
Зависимость обратной скорости от обратной концентрации субстрата (координаты Лайнуивера-Берка) для конкурентного ингибирования представлена на рисунке.

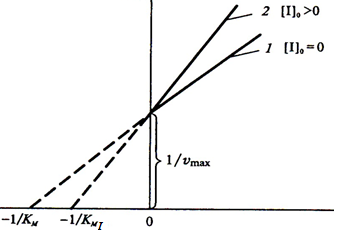
Неконкурентное ингибирование:

k₁ k₂

S +E ↔ ES → P

k_-1

E+I ↔ EI

ES+I ↔ ESI

Уравнение материального баланса по ферменту:

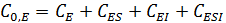
В случае равенства констант ингибирования:

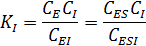
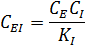
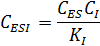
для начальной концентрации фермента можно записать:

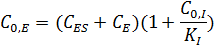
Используя уравнение для концентрации фермента:

и подставляя его в выражение для начальной концентрации фермента, можно получить:

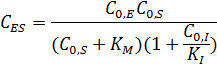
Начальная скорость реакции в присутствии ингибитора:

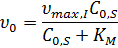
где 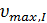– максимальная скорость реакции в присутствии ингибитора:

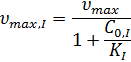
Константа ингибирования:

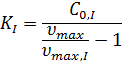
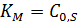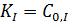Таким образом, изменяется максимальная скорость процесса, но константа Михаэлиса остается постоянной. Если , а то:

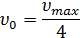
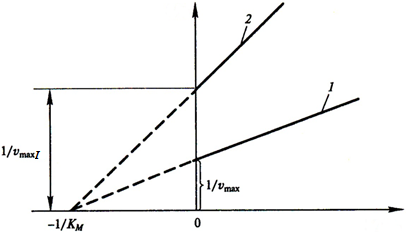
Зависимость обратной скорости от обратной концентрации субстрата для неконкурентного ингибирования представлена на рисунке.

Бесконкурентное ингибирование:

k₁ k₂

S +E ↔ ES → P

k_-1

ES+I ↔ ESI

Для начальной концентрации фермента можно записать:

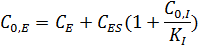
Начальная скорость реакции в присутствии ингибитора:

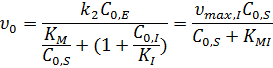
где 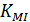– константа, зависящая как от начальной концентрации ингибитора, так и от константы ингибирования:

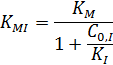
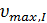– максимальная скорость реакции в присутствии ингибитора как и для неконкурентного ингибирования:

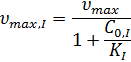
Зависимости обратной скорости от обратной концентрации субстрата для неконкурентного ингибирования представлены на рисунке