Трапецеидальные распределения

К трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона).

Равномерное распределение (рис. 11.1, а) описывается уравнением

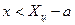0, и ;

р(х) (11.1)

, .

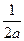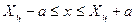С таким законом распределения хорошо согласуются погрешности от трения в опорах механических приборов, погрешности дискретности в ЦИП, неисключённые остатки СтП, отклонения размеров отверстия и вала.

Трапецеидальное распределение (рис.11.1, б) образуется как композиция двух равномерных распределений, но ширина их различна:

0, , ;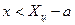

, ;

, ;

, .

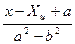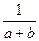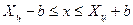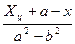По такому закону распределяется суммарная погрешность двух последовательно соединённых ИП.

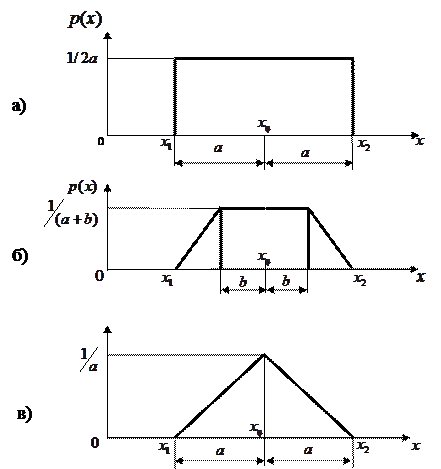
Рисунок 11.1 - Распределения: а – равномерное; б – трапецеидальное;

в – треугольное (Симпсона)

Треугольное (Симпсона) распределение (рис.11.1, в) – это частный случай трапецеидального, для которого размеры исходных равномерных распределений одинаковы:

0, , ;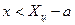

, ;

, ,

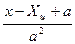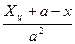где 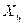, и 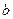– параметры распределения.

По такому закону распределены погрешности суммы (разности) двух равномерно распределённых СВ. Например, если отклонения размеров отверстия и вала распределены равномерно, то зазоры в пределах допуска зазора посадки отверстия и вала будут распределены по треугольному закону.

МО всехтрапецеидальных законов распределения 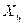=(Х₁+Х₂)/2. Медианы равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна .

СКО в зависимости от вида распределения определяется по формуле:

равномерное ;

трапецеидальное ;

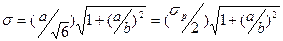треугольное 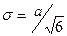.