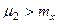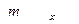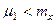Нормальное распределение (распределение Гаусса)

Этот закон, который называется распределением Гаусса, имеет наибольшее распространение, что объясняется центральной предельной теоремой теории вероятностей (теорема Ляпунова), утверждающей, что распределение СВ будет близко к нормальному всякий раз, когда результаты наблюдений формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

Для дифференциальной функции распределения нормальный закон имеет следующее выражение:

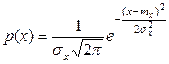, (11.2)

где р(х) – плотность вероятностей (плотность распределения);

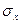- СКО результатов наблюдений;

m_x – МО;

Х – значение СВ.

Графически эта функция представлена на рис. 11.2 для различных значений СКО ().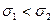

Из рис.11.2 и уравнения (11.2) можно заключить:

плотность вероятностей имеет max при x=m_x;

с увеличением погрешности 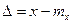независимо от знака (функция чётная) плотность вероятности стремится к 0;

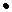с увеличение СКО вероятность больших отклонений увеличивается, т.е. размеры рассеиваются в более широком диапазоне ();

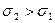абсцисса, соответствующая МО = 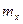, называется центром рассеивания (центром распределения) результатов;

изменение параметра 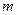_x= 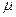не изменяет форму кривой нормального распределения р(х), а приводит к её сдвигу вдоль оси x (вправо, если 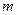_x возрастает и влево, если 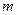_x убывает).

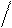
Рисунок 11.2 - Кривые нормального распределения ()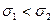

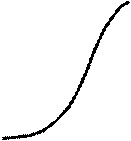
Интегральная функция нормального распределения результатов наблюдений имеет вид

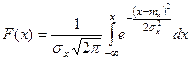, (11.3)

графики которой мы рассматривали ранее (рис. 10.1).

Учитывая, что при полном исключении СтП 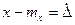и что 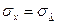, можно для дифференциальной функции распределения СП записать уравнение

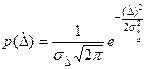
На рис. 11.3 изображены кривые нормального распределения СП для различных значений СКО (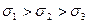). Из рисунка видно, что с увеличением СКО распределение СП всё более расплывается, вероятность появления больших погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.

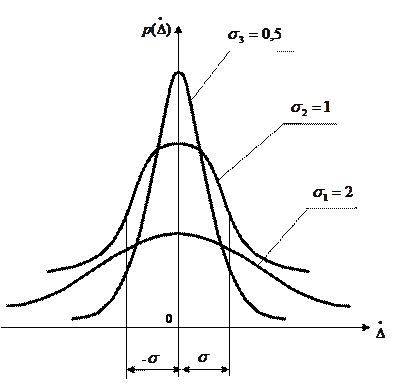
Рисунок 11.3 - Кривые нормального распределения СП (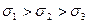).