
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормированный нормальный закон распределения. Интеграл Лапласа
|
|
При введении новой переменной 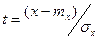 из (11.3) получается нормированное нормальное распределение, интегральная и дифференциальная функция которого соответственно равны:
из (11.3) получается нормированное нормальное распределение, интегральная и дифференциальная функция которого соответственно равны:
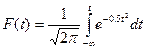 (11.5)
(11.5)
и
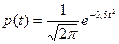 (11.6) Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функции нормированного нормального распределения сведены в таблицы 5, 6 [1], или П1, П2 [2].
(11.6) Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функции нормированного нормального распределения сведены в таблицы 5, 6 [1], или П1, П2 [2].
Определённый интеграл с переменным верхним пределом
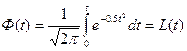 (11.7)
(11.7)
называют интегралом (функцией) Лапласа. Для неё справедливы следующие равенства:
с увеличение СКО увеличивается рассеивание результатов наблюдения  ;
; 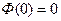 ,
, 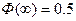 ;
; 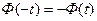 .
.
Функция Лапласа (ее иногда называют стандартной функцией) используется для определения значений интегральной функции нормального распределения, которая связана с интегралом Лапласа формулой
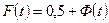 (11.8)
(11.8)
Поскольку интеграл в (11.3) не выражается через элементарные функции, то его значения для различных t (11.5) сведены в таблицу (см. приложение 1 [4] или табл. 9 [14]) с дискретностью 0, 01. С помощью указанных таблиц легко определяются значения интегральной функции нормального распределения при любых 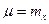 и
и 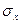 :
:
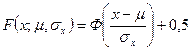 (11.9)
(11.9)