
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Точечные оценки законов распределения СВ
|
|
Рассмотренные выше законы распределения описывают поведение непрерывных СВ. На практике все результаты измерений и СП являются величинами дискретными, т.е. величинами 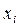 , возможные значения которых отделены друг от друга и поддаются счету. При использовании дискретных СВ возникает задача нахождения точечных оценок параметров их функций распределения на основании выборок – ряда значений
, возможные значения которых отделены друг от друга и поддаются счету. При использовании дискретных СВ возникает задача нахождения точечных оценок параметров их функций распределения на основании выборок – ряда значений 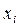 , принимаемых СВ
, принимаемых СВ 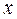 в
в 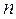 независимых опытах. Используемая выборка должна быть представительной, т.е. должна достаточно хорошо представлять пропорции генеральной совокупности.
независимых опытах. Используемая выборка должна быть представительной, т.е. должна достаточно хорошо представлять пропорции генеральной совокупности.
Оценка параметра называется точечной, если она выражается одним числом. Задача нахождения точечных оценок – частный случай статистической задачи нахождения оценок параметров функции распределения СВ на основании выборки. В отличие от самих параметров их точечные оценки являются СВ, причем их значения зависят от объема экспериментальных данных, а закон распределения – от законов распределения самих СВ.
Точечные оценки могут быть состоятельными, несмещенными и эффективными.
Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению оцениваемого параметра.
Несмещенной называется оценка, МО которой равно оцениваемому параметру.
Наиболее эффективной считают ту из некоторых возможных несмещенных оценок, которая имеет наименьшую дисперсию.
Требование несмещённости на практике не всегда целесообразно, т.к. оценка с небольшим смещением и малой дисперсией может оказаться предпочтительнее несмещенной оценке с большой дисперсией. На практике не всегда удается удовлетворить одновременно все три этих требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных точек зрения.
Существует несколько методов определения оценок, среди которых можно назвать метод моментов и метод наименьших квадратов. Однако наиболее распространен метод максимального правдоподобия, теоретически обоснованный математиком Р. Фишером. Этот метод приводит к ассимптотически несмещенным и эффективным оценкам с приближенно нормальным распределением.
Метод максимального правдоподобия сводится к отысканию таких оценок истинного 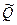 значения и
значения и 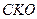
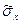 , при которых функция правдоподобия
, при которых функция правдоподобия
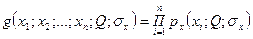 (11.10) Полученные оценки
(11.10) Полученные оценки 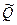 и
и 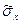 называются оценками максимального правдоподобия.
называются оценками максимального правдоподобия.
Точечной оценкой МО результата измерений является среднее арифметическое СА  значение измеряемой величины
значение измеряемой величины
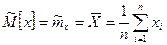 (11.11) При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по критерию наименьших квадратов.
(11.11) При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по критерию наименьших квадратов.
Точечная оценка дисперсии, определяемая по формуле
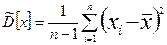 , (11.12)
, (11.12)
является несмещенной и состоятельной.
Оценка 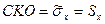 соответственно может быть найдена по формуле
соответственно может быть найдена по формуле
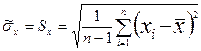 (11.13)
(11.13)
Величина Sx – есть оценка СКО отдельного наблюдения. Она характеризует разброс значений измеряемой величины относительно СА=  .
.
Величину Sx называют выборочным стандартом
Полученные оценки МО и СКО являются СВ. Это проявляется в том, что при повторениях серии из 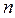 наблюдений каждый раз будут получаться различные оценки
наблюдений каждый раз будут получаться различные оценки 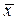 и
и 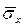 . Рассевание этих оценок целесообразно оценивать с помощью СКО
. Рассевание этих оценок целесообразно оценивать с помощью СКО 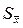 и
и 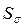 . Оценка СКО СА
. Оценка СКО СА
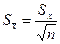 (11.14)
(11.14)
Оценка СКО СКО 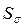
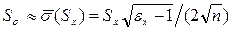 (11.15)
(11.15)
Отсюда следует, что относительная погрешность определения СКО может быть оценена как
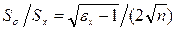 (1.16)
(1.16)
Она зависит только от эксцессов 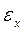 и числа наблюдений
и числа наблюдений 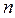 в выборке и не зависит от СКО, т.е. той точности, с которой производятся измерения.
в выборке и не зависит от СКО, т.е. той точности, с которой производятся измерения.
Следует запомнить, что наиболее распространенными оценками параметров распределения результатов наблюдений на практике являются точечные оценки МО, СКО и СКО СА.
