
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графический способ задания случайной дискретной величины.
|
|
Закон распределения случайной дискретной величины можно задать графически.
                                     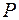
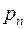 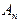
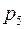 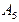
 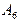
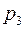 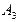
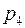 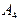
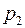 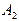
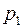 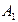
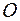 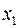 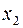 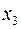 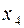 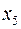 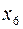 … … 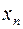 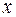
|
Пример. В денежной лотерее разыгрываются 20 билетов, из которых 5 выигрышей по 10 грн., 3 выигрыша по 20 грн. и 2 выигрыша по 50 грн. Найти закон распределения случайного выигрыша для владельца одного лотерейного билета, построить полигон распределения вероятностей.
Решение.
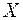
| ||||||
 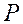
| 0, 5 | 0, 25 | 0, 15 | 0, 1 | ||
Для заданной случайной дискретной величины 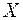 строим полигон распределения вероятностей. Для этого по горизонтальной оси откладываем возможные значения, а по вертикальной соответствующие им вероятности. Полученные точки строим полигон распределения вероятностей. Для этого по горизонтальной оси откладываем возможные значения, а по вертикальной соответствующие им вероятности. Полученные точки 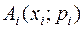 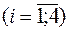 соединяем последовательно отрезками прямых. Полученная ломанная является многоугольником распределения вероятностей заданной случайной величины. соединяем последовательно отрезками прямых. Полученная ломанная является многоугольником распределения вероятностей заданной случайной величины.  
| ||||||
Пример. Каждый из двух стрелков стреляет по мишени один раз. Вероятность попадания для первого стрелка равна 0, 9, для второго стрелка – 0, 8.
Требуется:
а) найти закон распределения числа попаданий в мишень;
б) построить полигон распределения вероятностей.
Запишем условие задачи, вводя соответствующие обозначения.
Дано: событие 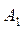 состоит в том, что попал первый стрелок;
состоит в том, что попал первый стрелок; 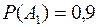 ;
;
событие 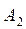 состоит в том, что попал второй стрелок;
состоит в том, что попал второй стрелок;  ;
;
 случайная величина
случайная величина 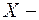 число попаданий в мишень.
число попаданий в мишень. 
 Требуется: а) найти закон распределения Х;
Требуется: а) найти закон распределения Х;
б) построить полигон распределения вероятностей.
Решение. а)
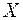
| ||||||
 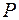
| 0, 02 | 0, 26 | 0, 72 | |||