
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сумма, разность, произведение случайных величин.
|
|
Пусть заданы законы распределения двух дискретных случайных величин: случайная величина 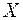 принимает значения
принимает значения 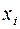 с вероятностями
с вероятностями 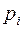
 , а
, а
случайная величина 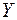 принимает значения
принимает значения  с вероятностями
с вероятностями 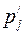
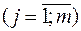 .
.
Определение. Две случайных величины 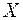 и
и 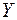 называются независимыми, если закон распределения любой из них не зависит от того, какое возможное значение приняла другая величина. В противном случае случайные величины называются зависимыми.
называются независимыми, если закон распределения любой из них не зависит от того, какое возможное значение приняла другая величина. В противном случае случайные величины называются зависимыми.
Если случайные величины 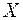 и
и 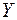 независимы, то независимы любые события
независимы, то независимы любые события 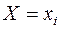
 и
и 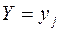
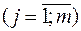 , а поэтому
, а поэтому
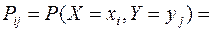
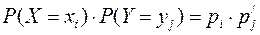 ,
,
если случайные величины 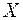 и
и 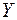 зависимы, то
зависимы, то
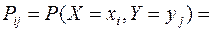
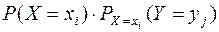 .
.
Примером двух независимых величин могут служить 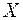 – размер выигрыша
– размер выигрыша
в одной лотерее, а 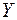 – размер выигрыша в другой.
– размер выигрыша в другой.
Аналогично определяется независимость событий 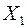 ,
, 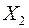 ,...,
,..., 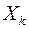 .
.
Определение. Случайные величины 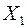 ,
, 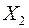 ,...,
,..., 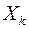 называются взаимно независимыми, если закон распределения любой из них не изменяется в зависимости от того, какие возможные значения приняли другие случайные величины.
называются взаимно независимыми, если закон распределения любой из них не изменяется в зависимости от того, какие возможные значения приняли другие случайные величины.
Будем в дальнейшем рассматривать только независимые случайные величины 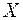 и
и 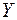 .
.
Определение. Суммой двух случайных величин 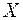 и
и 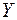 называется случайная величина
называется случайная величина 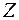 , возможными значениями которой являются допустимые суммы
, возможными значениями которой являются допустимые суммы 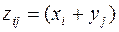
 , а вероятности этих значений находятся по формуле
, а вероятности этих значений находятся по формуле
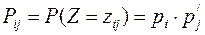 .
.
Аналогично определяются такие действия как разность и произведение двух случайных величин.
Определение. Разностью (произведением) двух случайных величин 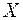 и
и 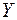 называется случайная величина
называется случайная величина 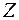 , возможными значениями которой являются допустимые разности
, возможными значениями которой являются допустимые разности 
 (произведения
(произведения 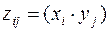
 ), а вероятности этих значений находятся по формуле
), а вероятности этих значений находятся по формуле
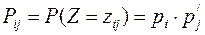 .
.
Введенные операции над случайными величинами можно обобщить на любое конечное количество случайных величин.
Пример. Заданы законы распределения двух дискретных случайных величин.
Таблица 11. Таблица 12.
| 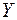
| ||||||
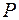
| 0, 1 | 0, 3 | 0, 6 | 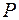
| 0, 2 | 0, 8 |
Найти закон распределения случайной величины 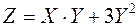 .
.