
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Лагранжа
|
|
Теорема. Любую квадратичную форму с помощью невырожденного линейного преобразования неизвестных можно привести к виду, в котором коэффициент при квадрате первой переменной отличен от нуля.
Доказательство. Рассмотрим квадратичную форму 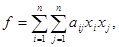 где
где 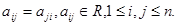 Если а 11
Если а 11 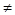 0, то утверждение доказано. Если а 11 = 0, но, скажем а 22
0, то утверждение доказано. Если а 11 = 0, но, скажем а 22 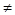 0, то изменим нумерацию неизвестных:
0, то изменим нумерацию неизвестных:
x 1 = y 2, x 2 = y 1, x 3 = y 3, … xn = yn.
Матрица этого линейного преобразования имеет вид:
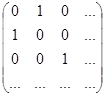 ,
,
невырожденная, так ее определитель равен -1. В преобразованной квадратичной форме коэффициент при у 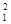 отличен от нуля.
отличен от нуля.
Пусть теперь коэффициенты при квадратах всех переменных равны нулю, но а 12 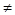 0. Тогда невырожденное линейное преобразование
0. Тогда невырожденное линейное преобразование
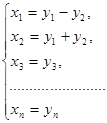
приводит квадратичную форму к виду, в котором коэффициент при у 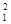 отличен от нуля. Если же коэффициенты при квадратах всех переменных равны нулю и а 12 = 0, но
отличен от нуля. Если же коэффициенты при квадратах всех переменных равны нулю и а 12 = 0, но 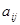
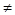 0, то изменив нумерацию переменных, сведем задачу к предыдущему случаю. ■
0, то изменив нумерацию переменных, сведем задачу к предыдущему случаю. ■
Квадратичная форма имеет канонический вид, если в ее записи нет слагаемых с произведениями неизвестных, т. е. 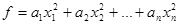 .
.
Теорема. (Лагранжа). Любую квадратичную форму с помощью невырожденного линейного преобразования неизвестных можно привести к каноническому виду.
Доказательство. С помощью невырожденного линейного преобразования приведем квадратичную форму f к виду, в котором а 11 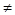 0. Все слагаемые, содержащие х 1, соберем в одну скобку и дополним эту скобку до полного квадрата, получим
0. Все слагаемые, содержащие х 1, соберем в одну скобку и дополним эту скобку до полного квадрата, получим
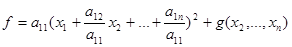 ,
,
где оставшиеся слагаемые образуют квадратичную форму g(x 2, …, xn) от неизвестных х 2, …, хn. Невырожденное линейное преобразование неизвестных

приводит квадратичную форму к виду
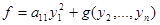 .
.
Повторив рассуждения, с учетом того, что последовательное выполнение невырожденных линейных преобразований вновь невырожденное линейное преобразование, получим утверждение теоремы. ■
Пример. Приведите с помощью невырожденного линейного преобразования неизвестных к каноническому виду квадратичную форму f = 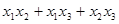 .
.
Линейное преобразование 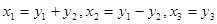 приводит квадратичную форму к виду
приводит квадратичную форму к виду 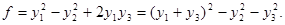 А линейное преобразование
А линейное преобразование 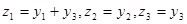 приводит к виду
приводит к виду 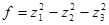 . Найдем сквозное линейное преобразование
. Найдем сквозное линейное преобразование 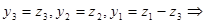
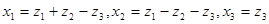 . Оно невырожденное, так как определитель матрицы линейного преобразования
. Оно невырожденное, так как определитель матрицы линейного преобразования
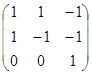
равен – 2, то оно невырожденное.
Ответ: невырожденное линейное преобразование неизвестных 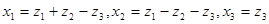 приводит форму к каноническому виду
приводит форму к каноническому виду 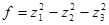
Квадратичная форма с действительными коэффициентами имеет нормальный вид, если в ее записи нет слагаемых с произведениями неизвестных, а квадраты переменных входят с коэффициентами 1 или -1 или совсем не входят. После изменения нумерации переменных нормальный вид можно переписать так: вначале идут коэффициенты 1, затем -1, а затем нули,
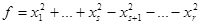 .
.
Теорема. Любую квадратичную форму с помощью невырожденного линейного преобразования неизвестных можно привести к нормальному виду.
Доказательство. Ограничимся доказательством возможности преобразования канонического вида 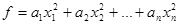 в нормальный вид с помощью невырожденного линейного преобразования:
в нормальный вид с помощью невырожденного линейного преобразования:
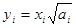 , если ai > 0;
, если ai > 0; 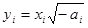 , если ai < 0;
, если ai < 0; 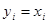 , если ai = 0. ■
, если ai = 0. ■