При этом отношение

l(y I i) = p(y I i)/p(y) (2.3)

называют отношением правдоподобия выборки у для элемента i заданного алфавита, функцию р(у I i) - функцией правдоподобия значений i.

Соотношения (2.2) позволяют перейти к алгоритмам классификации (в порядке нарастания общности): 1) максимума правдоподобия; 2) максимума послеопытной вероятности; 3) минимума среднего риска.

Алгоритм максимума правдоподобия соответствует принятию решения по максимуму (2.2) в предположении равновероятного появления объектов раз­личных классов Pi = 1/M = const. Тогда оценка 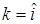номера класса i на­ходится из соотношения

k = arg max _i p(y I i) или k = arg max _i l(y I i). (2.4)

Алгоритм максимума послеопытной вероятности рассчитан на произволь­ные априорные вероятности P _i появления объектов различных классов. Он имеет вид

k = arg max _i [ P_ip(y I i) ] или k = arg max _i [ P_il(y I i) ] (2.5)

Алгоритм минимума среднего риска учитывает неодинаковую значимость различных ошибок и правильных решений для потребителя информации. В предположении " полупростой" матрицы стоимостей (разд. 1.9) он имеет вид

k = arg max _i [ r_iP_ip(y I i) ] или k = arg max _i [ r_iP_il(y I i) ] (2.6)

где r_i - неодинаковые в общем случае " премии" за правильные решения.

2.2.2. МУЛЬТИПЛИКАТИВНЫЕ БАЙЕСОВСКИЕ АЛГОРИТМЫ И ИХ ЧАСТИЧНАЯ

ПАРАМЕТРИЗАЦИЯ

Случайные реализации выборок сводятся в ряде случаев к совокупностям подвыборок у_v, v = 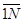с независимыми случайными флюктуациями. Это имеет место при сочетании узкополосного зондирования с широкополосным или многочастотным, при многопозиционной работе и т.д. В соответствии с правилом перемножения вероятностей алгоритмы (2.6) можно привести к мультипликативной форме:

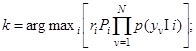(2.7)

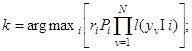(2.8)

Вариант алгоритма (2.8) следует из варианта (2.7) после деления оптими­зируемого выражения на произведение не зависящих от i и не влияющих, следовательно, на оптимизацию условных плотностей вероятности .

Частичная параметризация алгоритмов (2.7) - (2.8) связана с тем, что часть подреализаций 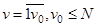, используют обычно для измерения па­раметров цели как признаков ее распознавания. Если известны априорные плотности вероятности 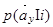распределений параметра 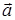для каждого i- го класса объектов, то входящие в (2.7) функции правдоподобия решений о классах 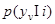можно связать с функциями правдоподобия значений парамет­ра 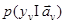, так что

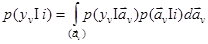(2.9)

Функция же правдоподобия значений параметра 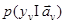связана с послеопытной плотностью вероятности его значений Эта связь

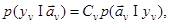
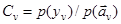(2.10)

вытекает из формулы умножения вероятностей при совмещении событий y _v и .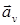

Входящую в (2.10) величину С_v поcле приема реализации y_v при изме­рении 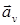по максимуму правдоподобия можно считать фиксированной вели­чиной. Действительно, значение p(y_v) после приема реализации y_v фиксиро­вано. В условиях же измерения 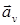по максимуму правдоподобия (безотносительно к гипотезам о значениях i) допустимо принять .

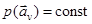Если ввести плотность вероятности f(ε) ошибок измерения 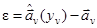, то входящую в (2.9) послеопытную плотность вероятности значений парамет­ра можно представить в виде

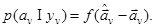
В силу (2.9) - (2.10) функции правдоподобия решений о классе можно придать вид

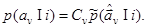(2.11)

Согласно (2.11) она пропорциональна значению для 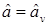априорнойплотности вероятности оценок параметра 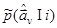с у четом ошибок измерения: Значение 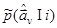определяется интеграломсвертки

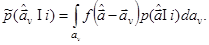
В нем 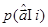– априорная плотность вероятности значений параметра. При идеально точном измерении 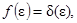где 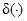- дельта-функция. Тогда 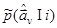= 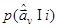и

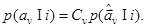
Алгоритмы распознавания (2.7) –(2.8) заменяются в результате пол­ученных соотношений (2.9) – (2.11) единым мультипликативным алгорит­мом:

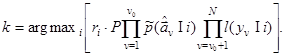(2.12)

Из него исключены, как и ранее, не зависящие от i множители заключен­ного в квадратные скобки выражения. Знаки " тильда" при априорных плотностях вероятности параметров (признаков распознавания) учитывают, как и в (2.11), конечную точность оценок .

Обычно векторный признак 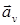, оцениваемый по некоторой реализации y_v, разбивается на несколько скалярных и векторных признаков с неза­висимыми их флюктуациями и флюктуациями их оценок. Сомножители первого из произведений (2.12) сами становятся тогда произведениями нескольких аналогичных сомножителей. Чтобы не усложнять формулу (2.12), условимся сохранять ее вид и в этом случае, условно сводя увеличение общего числа признаков к увеличению числа независимых подреализаций v₀ и N.

2.2.3 АДДИТИВНЫЕ ЧАСТИЧНО ПАРАМЕТРИЗОВАННЫЕ БАЙЕСОВСКИЕ АЛГОРИТМЫ

Переход от мультипликативных алгоритмов к аддитивным основан на мо­нотонности логарифмической функции. Логарифм произведения в квадратных скобках (2.12) достигает максимума одновременно с самим этим произведени­ем. Он сводится при этом к сумке логарифмов сомножителей, что упрощает вычисления. Отсюда приходим к частично параметризованным аддитивным ал­горитмам распознавания

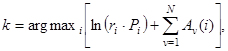(2.13)

где 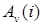- неоднородные слагаемые.

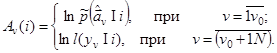(1.4)

Аддитивные алгоритмы, наряду с мультипликативными, применимы не только при независимости подреализаций y_v, но и при независимости оши­бок измерений параметров 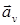по одной и той же реализации или подреализации.

2.2.4. ПРИМЕРЫ ЭЛЕМЕНТОВ БАЙЕСОВСКИХ АЛГОРИТМОВ

Элементы алгоритмов, связанные с измерением траекторных параметров объектов в тропосфере

Маневренность тропосферных объектов, большая по сравнению с космиче­скими объектами, сужает совокупность признаков распознавания. Входящие в (2.13) - (2.14) априорные распределения параметров 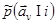(с учетом оши­бок измерения) приходится задавать описаниями общего вида. Последние мо­гут относиться к одномерным и многомерным, односвязным и многосвязным, ступенчатым и непрерывным, негауссовским и гауссовским распределениям.

Обобщая распределение вектор-столбца скоростей и высот цели на плоско­сти v - Н (рис.1.1), введем многомерные односвязные ступенчатые негауссовское распределение и распределение его логарифма, равномерные в преде­лах области, заданной линейными ограничениями,

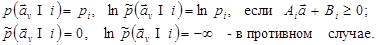(2.15)

Здесь 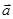– вектор-столбец размера 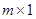, В _i – вектор-столбец размера 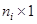. А _i - матрица размера 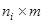, п_i - число ограничений на скалярные параметры вектора 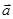. Значение 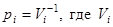– объем многогранника, определяемого ограничениями. Выполнение приведенных матричных неравенств понимается в смысле выполнения всех скалярных неравенств, на которые они распадаются. При переходе от односвязных распределений к многосвязным ог­раничения (2.15) и величины р_i для каждой из односвязных подобластей под­бираются раздельно.

Примером одномерного, непрерывного негауссовского распределения явля­ется обобщение гауссовского:

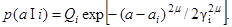(2.16)

Здесь a _i – условное (для целей i -го класса) математическое ожидание параметра а: γ i – полуширина распределения на уровне 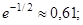μ – характеристика формы распределения. Кривая – гауссовская при μ =1, двусторонняя экспоненциальная при μ =1/2 и приближается к прямоугольной с увеличением μ при 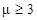. Нормирующий множитель Q i выражается через гамма-функцию:

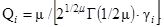(2.17)

Примером непрерывного трехмерного односвязного распределения для а= \уНа\, где а - полное ускорение, является распределение 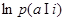вида

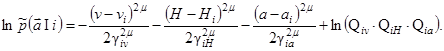(2.18)

Трехмерное распределение (2.18) предполагает независимость априорных одномерных распределений v, Н, а в. Вводя в (2.18) слагаемые в виде сте­пеней линейных комбинаций величия v, Н, а, можно учесть взаимную за­висимость распределений этих величин.