Непараметрические алгоритмы многоальтернативного распознавания

Составляются эвристически в расчете на неизвестные заранее статистические распределения признаков объектов различных классов. К их числу мож­но отнести, в частности, различные варианты алгоритмов вычисления расстояний и голосования.

2.3.1. АЛГОРИТМЫ ВЫЧИСЛЕНИЯ РАССТОЯНИЙ

К ним относятся алгоритмы минимума расстояний и алгоритмы " ближайших соседей" [10 - 13, 17].

Алгоритмы минимума расстояний. Предусматривают принятие реше­ния k о классе объекта 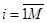по минимуму расстояний d_i или их квад­ратов 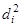от точки многомерного пространства признаков, определяемой оценочным вектором 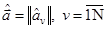до точек 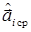, соответствующих ус­ловным средним значениям векторов признаков для различных классов объек­тов i. Иначе,

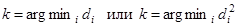(2.21)

В силу монотонности квадратичной функции оба приведенных равенства равносильны. Об условных распределениях вектора признаков для различных классов достаточно знать только их средние значения. Мера же расстояния может видоизменяться. Могут использоваться евклидово расстояние, расстоя­ние Махалонобиса, расстояние в пространстве обобщенных признаков.

Евклидово расстояние определяется из соотношения

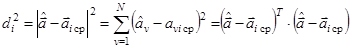, (2.22)

аналогично соответствующему соотношению для трехмерного пространства N =3. Будучи эвристическим для произвольных распределений вероятностей признаков, алгоритм (2.21), (2.22) совпадает с байесовским алгоритмом для гауссовского распределения признаков при условии их независимости (некоррелированности) и нормирования признаков из условия единичной дисперсии.

Расстояние Махалонобиса определяется в предположении, что известны как условные средние значения, так и соответствующие корреляционные матрицы Ф _i для векторов признаков объектов различных классов:

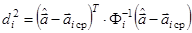(2.23)

Алгоритм (2.21), (2.23) с точностью до логарифмического слагаемого совпадаетпри этом с оптимальным байесовским алгоритмом для гауссовской статистики признаков, где признаками служат отсчеты принимаемой выборки. Если различия в разбросах признаков различных классов после их нормирования несущественны, то Ф _i = Ф. Если при этом Ф = I, где I – единичная матрица, то расстояние Махалонобиса переходит в евклидоворасстояние.

Обобщенные признаки. Вводятся на основе диагонализации входящей а (2.23) обратной корреляционной матрицы (здесь считается, что Ф _i = Ф).

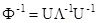. (2.24)

В (2.24) Λ - диагональная матрица собственных чисел λ _i, а U - унитарная матрица. Расстояние (2.23) переходит при этом в

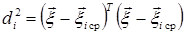, (2.25)

где 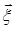– векторы признаков [11, 58, 59]:

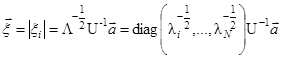. (2.26)

Обобщенные признаки некоррелированы, имеют единичные дисперсии и для них расстояние Махалонобиса совпадает с евклидовым.

Алгоритмы " ближайших соседей". Для точки 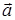, определяемой оценочным вектором признаков, находится L ближайших к ней точек из имеющихся в памяти ЭВМ. В этой памяти собраны экспериментальные реализации вектора признаков при предъявлении объектив различных классов. Наблюдаемый объект относят обычно к тому классу, к которому относится 6ольшинство из L его " ближайших соседей", т.е.

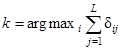(2.27)

Здесь δ _ij - символ Кронекера, δ _ij =1 при i=j и δ _ij =0 при i¹ j. Он при­нимает единичное значение, если j -й ближайший сосед принадлежит i -му классу, и нулевое - в противном случае. Мерой близости " соседей" служат рас­стояния, вычисляемые тем или иным образом. При I.= 1 алгоритм " ближай­ших соседей" переходит в алгоритм " ближайшего соседа". Доказано, что веро­ятности ошибок распознавания при 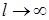совпадают с байесовскими, а при L =1 не более чем в два раза превышают их [10].

Алгоритмы " ближайших соседей" не требуют подбора и оценивания па­раметров вероятностных распределений - они непараметрические (даже усред­нения экспериментальных отсчетов, как и в алгоритмах минимума расстояний, не требуется). Их можно считать в то же время результатом перехода от параметрических алгоритмов (разд. 2.2.2 - 2.2.3) при использовании которых нужны оценки плотностей вероятности . Для фиксированного элементарного объема в пространстве признаков эти оценки определяются числом попадающих в него реализаций соответствующих классов i.

2.3.2. АЛГОРИТМЫ ГОЛОСОВАНИЯ

Относятся к многоэтапным алгоритмам принятия решений. На первом эта­пе независимо принимаются предварительные многоальтернативные 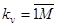решения по отдельным признакам или группам признаков 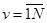. В роли решений по группам признаков могут выступать решения различных источников информации (РЛС). На втором этапе решения объединяются по взвешенному (с учетом достоверности) или по простому большинству голосов [2, 6, 20, 60].

Алгоритм извещенного голосования. Имеет вид

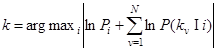. (2.28)

Структура алгоритма (2.28) аналогична структуре байесовского алгоритма (2.13) - (2.14), но упрощена по сравнению с ним. Реализации измеряемых параметров 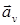и принимаемые реализации 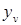, имеющие непрерывный закон распределения, заменены реализациями предварительных решений в виде слу­чайных чисел k_v, имеющими дискретный закон распределения. Условные плотности вероятности 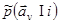и отношения правдоподобия 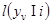замене­ны поэтому на вероятности 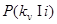, Упрощение касается также использования в (2.15) простых стоимостей решений r_i =r когда сопоставление по ним теряет смысл.

Предполагается, что МхМ матрицы условных вероятностей решений 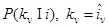по каждому признаку v заранее установлены путем моделирования натурного эксперимента или расчета. Матрица соответствующих лога­рифмов введена в долговременную память ЭВМ. При эффективных признаках распознавания диагональные элементы матриц заметно больше недиагональ­ных. После получения каждого предварительного решения 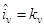в опера­тивную память пересылается из долговременной k_v -й столбец соответствую­щей v -й матрицы, который и используется для принятия окончатель­ного решения (2.28).

Алгоритм простого голосования. Отличается от предыдущего заменой М различающихся матриц 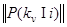на одинаковые и более простые единич­ные матрицы 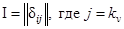. Иначе все наибольшие диагональные элементы заменены единицами, а все меньшие, недиагональные элементы - нулями. Пренебрегают, кроме того, возможным неравенством доопытных вероятностей различных классов P_i. Алгоритм сводится к подсчету и выявлению максимума голосов " за" по отдельным признакам (группам признаков) v:

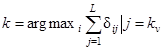. (2.29)

Алгоритм (2.29) не предусматривает введения и оценивания параметров каких-либо распределений и является полностью непараметрическим, в отличие от (2.28), в который входили еще параметры Р_i и 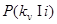. Однако определенный произвол построения алгоритма (2.29) и даже алгоритма (2.28) не может не сказаться на качестве распознавания.

Небезынтересно, что алгоритм простого голосования можно свести к одному из алгоритмов минимума расстояний, а именно, к алгоритму минимума расстояний Хемминга. Для этого достаточно представить (2.29) в виде

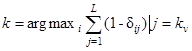(2.30)

где вместо подсчета и выявления максимума числа голосов " за" подсчитывается и минимизируется число голосов " против". Входящую и (2.30) сумму называют расстоянием Хэмминга в дискретизированном пространстве параметров (призна­ков) от принятой реализации до произвольной реализации i.

Алгоритмы " вычисления оценок" (АВО). Составляют класс алгоритмов, предложенный в 1971 г. Ю.И. Журавлевым [9, 50] для распознавания классов объектов по большому числу признаков с небольшими выделительными затратами. Окончательное решение принимается по большинству голосов (" оценок"), полученных при выявлении сходства отдельных групп признаков классифицируемого объекта с аналогичными группами признаков конкретных объектов каждого класса. Сходство выявляется на основе промежуточных голосований " да", " нет" без права или с правом воздерживаться. После каждого из промежуточных голосований предусматриваются пороговые процедуры. Итоговое голосование по всем объектам каждого класса и всем группам при­знаков - взвешенное, с возможной дополнительной пороговой процедурой, например, для разности максимального и наибольшего из конкурирующих с ним числа голосов.

Более поздний " алгебраический подход" Ю.И. Журавлева предусматривает составление улучшенных алгоритмов из менее совершенных по правилам некоторой алгебры [18, 51].