Вектор комплексной огибающей радиолокационного сигнала находится по формуле

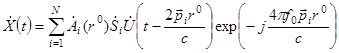. (4.3)

Здесь 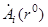- поляризационная матрица рассеяния i -го отражателя; 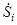- поляризационный вектор падающей волны; N - число освещенных отражателей; r ° - единичный вектор падающего поля; 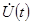комплексная огибающая сигнала на выходе устройства оптимальной обработки; 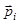- радиус-вектор фазового центра i -го отражателя; f о - несущая частота; с - скоро­сть света в свободном пространстве.

В процессе вычисления находят с помощью ЭВМ: а) векторы r ⁰ для различных ориентации цели; б) число N блестящих элементов и их координаты с учетом эффектов затенения; в) вклад каждого элемента в сумму (4.3); г) сумму вкладов (4.3).

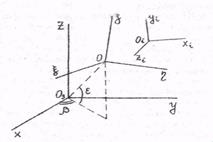
Рис. 4.1. Системы координат наземного локатора О_зхуz, воздушной цели Оξ η ζ и i-й аппроксимирующей поверхности О _i x _i y _i z _i

На рис. 4.1 показаны О_з xyz и Оξ η ζ – системы координат наземного локатора и воздушной цели; β - азимут и ε - угол места целя в первой системе. Не показаны Ψ, Θ, γ – углы курса, тангажа и крена цели во второй системе. Вошедший в (4.3) единичный вектор r ° имеет в первое системе составляющие cos ε ּ cos β, cos ε ּ sin β, sin ε и определяется во второй системе выражениями

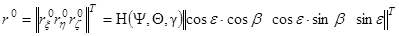; (4.4)

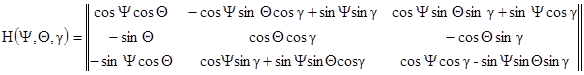(4.5)

Учет особенностей цели. Ее поверхность аппроксимируется на основе чертежа совокупностью участков поверхностей второго порядка F_i (ξ, η, ζ)=0. Объекту принадлежат лишь точки i -й поверхности (i = 1, 2,..., n), которые лежат внутри неких ограничивающих ее поверхностей 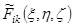, где k =1, 2,..., K_i - номер (K_i – число поверхностей, ограничивающих i -ю поверхность).

Кромки крыльев, киля и стабилизатора задаются клиньями, параметры каждого из них - длина и угол в радианах (см. пункт 5 приложения 4).

Изломы на стыке поверхностей второго порядка аппроксимируются клиньями с изогнутыми ребрами. При этом задают радиус кривизны клина и его внешний раскрыв (см. пункт 5 приложения 4).

Положение воздухозаборников двигателей задают координатами центров входных отверстий. Учитываются параметры двигателей: форма поперечного сечения воздухозаборника, его глубина, число, форма и размеры лопаток компрессора. Кромки воздухозаборника аппроксимируют частями тора или тонкими клиньями (пункты 3, 4 приложения 4).

Координаты центров бортовых антенн и единичные векторы нормали к апертурам антенн описывают положение и ориентацию антенн в системе ко­ординат цели. Задаются параметры их раскрыва, рабочая длина волны, фокусное расстояние (для зеркальных антенн), параметры облучателя и некоторые другие характеристики.

Для поверхностей, покрытых радиопоглощающими материалами, задают толщину покрытия, комплексные относительные проницаемости материала, степень неоднородности покрытия, форму укрывае­мой поверхности или же экспериментальную зависимость коэффициента отражения от углов облучения и наблюдения.

Каждая поверхность второго порядка (ограничивающая в том числе) задается предварительно в своей местной (канонической) системе координат О _i x _i y _i z _i параметрами уравнений F_i (x _i, y _i, z _i)=0, .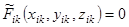

Например, участок цилиндрической поверхности, заданной уравнени­ем F_i (x _i, y _i, z _i)= 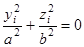. может ограничиваться парой плоскостей, перпендикулярных его оси, описываемых уравнением 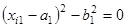. В этих выражениях а, а ₁ и b, b ₁ – параметры поверхностей.

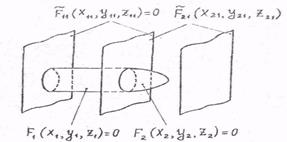
Рис. 4.2. Простейшая цель в виде сочленения, цилиндра (F₁) с эллипсоидом (F₂) и соответствующие ограничивающие пары плоскостей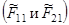

Рис. 4.2 поясняет изложенное на примере простейшей цели в виде сочленения цилиндра с эллипсом. Блестящая точка на поверхности эллипсоида проверяется на ее местонахождение между парой ограничивающих плоскостей 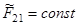. Блестящая образующая на поверхности цилиндра проверяется на ее местонахождение между парой плоскостей .

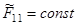Преобразование координат блестящей точки из местной системы координат в систему координат цели. Описывается выражением

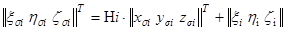(4.6)

Здесь Н _i - матрица перехода от системы Оξ η ζ к системе О _i x _i y _i z _i раз­мера 3х3; ξ _i η _i ζ _i - координаты точки О _i в системе Оξ η ζ. Пересчеты век­тора r ° в местные системы координат проводятся согласно выражению r_i =H _ir °

Блестящие элементы при однопозиционной локации. Определяются точками стационарной фазы. Известно, что плоскость фронта волны является касательной к выпуклой поверхности F(х, у, z)= 0 в точке стационарной фа­зы. Иначе, единичный вектор r °, задающий нормаль к фронту волны, коллинеарен вектору grad F, откуда

(4.7)

где 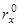, , 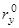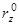– направляющие косинусы, являющиеся проекциями на коорди­натные оси вектора r °.

Аналитические выражения для нахождения координат блестящих элементов различных поверхностей второго порядка сведены в приложение 2.

Проверка затенения. Луч, проведенный из блестящей точки (ξ _σ η _σ ζ _σ ) некоторой аппроксимирующей поверхности в направлении на РЛС, не должен пе­ресекать (по Ю.В.Сопельнику) ни один из ограниченных участков других апп­роксимирующих поверхностей. Чтобы удостовериться в этом, следует подста­вить в уравнение i -й (проверяемой) поверхности второго порядка выражения прямой ξ = ξ _σ - r° ξ t, η = η _σ - r° η t, ζ = ζ _σ - r° ζ t. Полученное квадратное урав­нение аt² + bt + c = 0 решается относительно t.

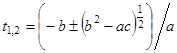. (4.8)

Здесь

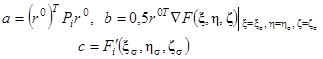(4.9)

где Р i – матрица 3х3 коэффициентов канонического уравнения i -й поверхности. Если уравнение (4.8) имеет хотя бы одно действительное положительное реше­ние, то данная " блестящая" точка затенена.

Проверка затенения " блестящих" образующих и кромок производится диск­ретно с шагом Δ l. Для плоской поверхности проверяется затенение центра каждой из элементарных площадок Δ S _i, на которые она разбита.

Расчет поляризационных матриц элементарных излучателей при од­нопозиционной локации. Осуществляется в соответствии с выражением 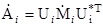. Здесь 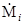– диагональная поляризационная матрица 2х2 в соб­ственном поляризационном базисе i -го отражателя с диагональными элементами 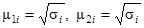; U _i - это матрица перехода от собственного поляризационного базиса i -го отражателя к поляризационному базису приемно-передающей антенны. Для линейно-поляризованной волны, падающей на пря­мую кромку, ее элементы равны U _{11 i} = U _{22 i} = cosφ _i, U _{21 i} = U _{22 i} = -sinφ _i, где φ _i – угол между вектором поляризации падающего поля и проекцией линии кромки на фронт волны. При вычислениях ЭП элементарных отражателей мож­но использовать формулы приложения 4, а также [74, 75, 99 - 101, 108 - 112].

4.3.3. ДИНАМИЧЕСКИЕ ЦИФРОВЫЕ МОДЕЛИ ВТОРИЧНОГО ИЗЛУЧЕНИЯ

Используют общие принципы цифрового моделирования [114, 116, 117], сочетая моделирование электродинамических процессов, кинематики движения целей и их элементов, статистики помех и методов обработки принимаемых ко­лебаний [1]. Учитывают, в частности, кинематику и динамику: а) детермини­рованного и случайного движения целей; б) движения элементов целей (лопа­ток компрессоров и турбин, лопастей винтов) относительно связанных с целями систем координат; в) неодновременного облучения элементов целей моделиро­ванными сигналами [1]. В развитие раздела 4.2.1 можно использовать методы математического моделирования для получения ряда важных характеристик вто­ричного излучения и определения показателей качества алгоритмов распознава­ния.

Варианты построения динамических моделей

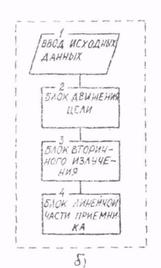
Показаны на рис. 4.3. Исходными данными в первом случае (рис. 4, 3, а) служат длина волны, поляризация приемно-передающей антенны, параметры зондирующего сигнала, самих целей, а также составляющие их траекторий (ре­гулярные и случайные).

В соответствии с рис. 4.3, а следовало бы моделировать: а) прохождение сигнала от РЛС к цели (блок 2); б) регулярное и случайное движения цели (блок 3); в) вторичное излучение цели (блок 4); г) прохождение сигнала от цели к РЛС (блок 5); д) работу линейной части приемного устройства (блок 6).

В предположении линейности среды распространения, процесса вторичного излучения и обработки сигнала модели роение упрощается. Моделируется по­следовательно (рис. 4.3, 6): а) регулярное и случайное движение цели (блок 2); б) расчет координат и амплитуд элементов матриц рассеяния блестящих точек цели (блок 3); в) работа линейной части приемника. В последнем блоке проводится согласно (4.3) расчет комплексной огибающей отраженного сигнала на выходе фильтра, согласованного с зондирующим сигналом. Описанная модель позволяет получать временные, частотные, поляризационные зависимости отраженных сигналов при различных значениях ширины спектра зондирующего сигнала.

Примеры моделирования приводились на рис. 1.2 - 1.8. 1.12 - 1.21.

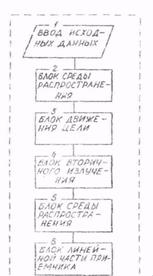
Рис. 4.3. Варианты построения динамических и цифровых моделей вторичного излучения: без учета (а) и с учетом (б) линейности среды распространения процесса вторичного излучения и обработки сигнала

4.4. МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ КАЧЕСТВА

РАДИОЛОКАЦИОННОГО РАСПОЗНАВАНИЯ

Подразделяются на: а) натурные; б) методы физического моделирования; в) методы математического моделирования. К определяемым показателям каче­ства работы систем распознавания относят матрицы условных вероятностей рас­познавания, а также полные вероятности ошибок распознавания при равномер­ном появлении целей различных классов для различных ракурсов, дальностей (отношений сигнал/шум), условий помеховой обстановки и т.д. Сопоставлению могут подлежать также: а) реализуемый алфавит распознаваемых классов це­лей; б) коэффициент сокращения зоны распознавания по целям i-го класса относительно зоны обнаружения; в) временные характеристики распознавания (периодичность и число обращений к цели); г) пропускная способность канала распознавания (например, число распознаваемых целей в минуту); д) аппара­турные затраты и вычислительная сложность; е) степень влияния на другие ре­жимы работы РЛС; ж) помехозащищенность от активных и пассивных помех; з) имитостойкость; и) вопросы электромагнитной совместимости при использо­вании специальных видов сигналов.

4.4.1. НАТУРНЫЕ МЕТОДЫ

Могут быть реализованы в полигонных экспериментах на РЛС с каналами радиолокационного распознавания по специальным методикам. Как и при лю­бых других испытаниях, должны быть заранее установлены оцениваемые пока­затели качества и способы их оценки; алфавит распознаваемых классов, а зна­чит, требуемые летные средства и средства траекторного анализа; порядок набо­ра, регистрации, отбраковки и обработки экспериментальных данных. Полезно сочетание натурного эксперимента и моделирования (см. разд. 4.2.2 и 4.3.3).

4.4.2. МЕТОДЫ ФИЗИЧЕСКОГО МОДЕЛИРОВАНИЯ

Возможно использование как электродинамического, так и акустического моделирования (см. разд. 4.2.2, 4.2.3). Последнее рассматривается как предва­рительная мера или как дополнение по отношению к методам натурных испы­таний. Используется для: а) определения показателей качества макетов устрой­ства распознавания; б) имитации возможной обстановки при натурных испыта­ниях РЛС с каналами распознавания (например, с помощью малоразмерных от­ражателей, поднимаемых на метеозондах); в) определения показателей качест­ва и сопоставления алгоритмов, использующих различные сочетания признаков распознавания (совместно с методами математического моделирования).

4.4.3. МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Наиболее оперативны и экономически выгодны для проведения предвари­тельных исследований. Могут использоваться для: а) сопоставления алгоритмов распознавания; б) сопровождения и обеспечения натурных испытаний, в) вы­явления и исследования новых признаков распознавания. В качестве данных для моделирования могут применяться данные натурных измерений, вспомога­тельных физического и математического моделирования.

Блок-схема математиче­ской модели для последнего случая приведена на рис. 4.4. Дополнительно к рис. 4.3, б введены: а) блок шумов и внешних помех с учетом ли­нейной частя приемника (блок 5); б) блок принятия решений (блок б); в) блок оценки результатов распозна­вания (блок 7). Блок шумов и внешних помех предназна­чен для моделирования рас­познавания на фоне внутрен­них шумов приемника, а так­же в условиях активных и пассивных помех. В блоке принятия решений моделируется алгоритм (или несколько разновидностей алгоритмов) распознавания. Перед блоком принятия решений в ряде случаев необходим блок выделения признаков распознавания. В этот блок могут входить, например, алго­ритмы получения одномерных или двумерных радиолокационных дальностных или дальностно-угловых портретов. Блок оценки результатов распознавания со­держит алгоритмы статистической обработки потока принимаемых решений с учетом условий распознавания и расчета показателей качества распознавания.

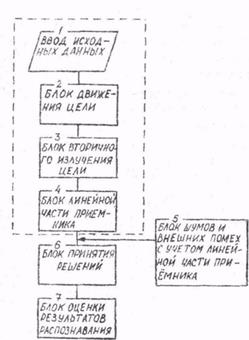
4.4. Блок-схема математической модели для определения показателей качества распознавания

4.4. ПРИМЕРЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ РАСПОЗНАВАНИЯ

ВОЗДУШНЫХ ЦЕЛЕЙ ПО СОВОКУПНОСТИ ПРИЗНАКОВ

Моделирование проводилось в соответствии с блок-схемой рис. 4.4. Модели целей составлялись в соответствии с методикой разд. 4.3.2. В зависимости от размера объекта модели содержали от тридцати до двухсот элементов. Модели­ровались различные варианты словарей признаков, алфавитов классов и алго­ритмов распознавания.

Вводились, в частности, следующие варианты словарей признаков: СП1 – корреляционная сумма (2.19) + эффективная площадь, полученные по ДП цели при одном обращении к ней пачкой широкополосных сигналов; СП2 - словарь признаков СП1 + эффективная площадь, измеренная по результатам 10 - 15 узкополосных зондирований; СПЗ - словарь признаков СП2 + признак, свя­занный с флюктуациями формы ДП внутри пачки широкополосных импульсов; СП4 - словарь признаков СП3 + траекторные признаки (скорость, высота и их первые производные по времени).

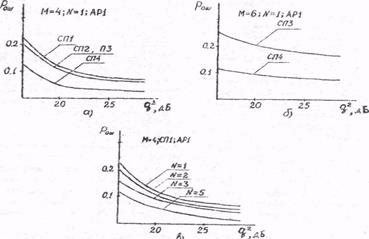
Рис.4.5. Результаты моделирования распознавания воздушных целей: а - для раз­личных словарей признаков СП1– СП4 и алфавит М = 4 (N=1, AP1); б – для различных словарей признаков СПЗ - СП4 и алфавита М = 6 (N=1, АР1); в – для различною числа обращений к цели широкополосным сигналом N = 1, 2, 3, 5 (М=4, СП1,.АР1)

Алфавит распознаваемых классов М = 4 включал в себя классы целей крупных, средних и малых размеров, а также малоразмерных целей с искусственно увеличенной эффективной площадью. В алфавит классов М = 6 дополнительно входили классы вертолетов и метеозондов. В каждый из распознаваемых классов входило от одного до трех типов целей.

Моделировалась работа следующих алгоритмов распознавания: АР1 – ад­дитивный частично параметризованный байесовский алгоритм (разд. 2.2); АР2 – алгоритм взвешенного голосования (2.28); АРЗ – алгоритм простого голосования (2.29); АР4 – алгоритм минимума расстояний (2.21). (2.22).

Приводимые ниже варианты зависимостей полной вероятности ошибки рас­познавания Р_ош (см. разд. 1.9) от отношения сигнал/шум q², дБ, рассчитаны лишь на качественное пояснение возможностей моделирования. Имеется в виду, что количественные параметры предполагаемых вариантов распознающих систем устанавливаются в ходе проектирования и здесь поэтому не уточняют­ся.

На рис. 4.5, а приведены зависимости Р_ош (q²) для различных вариантов словарей признаков СП1 - СП4, алфавита классов М = 4, одного обращения к цели широкополосным сигналом (N = 1) и алгоритма АР1.

На рис. 4.5, б показано влияние на Р_ош (q²) выбора словарей признаков СПЗ и СП4 пои расширенном алфавите классов М = 6 для алгоритма АР1.

Рис. 4.5, в иллюстрирует возможности повышения качества распознавания (сни­жение суммарной ошибки распознавания) при увеличении числа N обращений к цели широкополосным сигналом для алфа­вита М = 4, словаря признаков СП1 и алгоритма АР1.

На рис. 4.6 показано влияние на Р_ош (q²) выбора алгоритма распознавания АР1 - АР4 для алфавитаМ = 4, словаря признаков СП4 и для одного обращения к цели широкополосным сигналом.

Некоторые особенности моделирования распознавания на основе двумерных дальностно-азимутальных портретов целей обсуждаются в приложении 5, а на основе нейрокомпьютерных и нейробайесовских алгоритмов - в приложении 6.

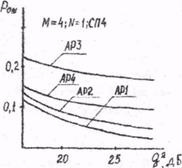
Рис. 4.6. Результаты моделирования распознавания М = 4-х классов воздушных целей различными алгоритмами (АР1 - АР4) при одном (n = 1) обращении к цели широкополосным сигналом для наибо­лее широкого из исследовавшихся словаря признаков СП4