Пример расчета физической системы в Maple

Цель данной лекции состоит в построении в Maple конкретного примера расчета модельной квантовой системы: прохождение частицы через одномерный прямоугольный потенциальный барьер [2, с. 101–102]. На этой задаче можно многому научиться. Детальный разбор такой задачи и доведение ее «до числа» позволит существенно продвинуться в изучении Maple и выйти на некий минимальный уровень практического владения системой для расчета и моделирования физических систем.

Теоретические сведения. Рассмотрим частицу массы m, способную перемещаться по оси x под действием некоторого потенциала 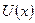[2, с. 84]. Уравнение Шредингера записывается в виде:

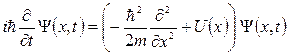. (1.2)

Потоки частиц моделируются стационарными состояниями. Если E есть энергия стационарного состояния (энергия частицы), то волновая функция имеет вид:

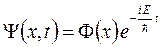, (1.3)

причем функция является решением стационарного уравнения Шредингера (штрих обозначает дифференцирование по координате)

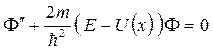. (1.4)

Требуется найти решения данного уравнения, ограниченные, непрерывные и дифференцируемые во всем интервале .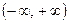

Рассмотрим случай прямоугольного потенциального барьера, который описывается кусочно-постоянной потенциальной функцией

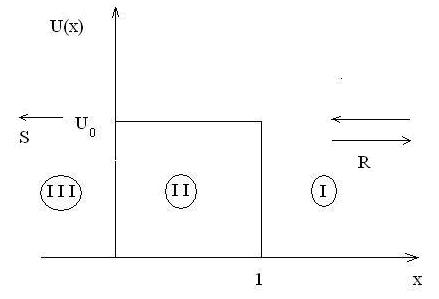
Рис. 1.4. Прямоугольный потенциальный барьер

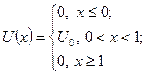(1.5)

Весь интервал x разбивается на три области, пронумерованные на рисунке 1.4. В каждой области частица описывается своей волновой функцией, обозначим их как 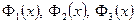. Они удовлетворяют уравнениям

,

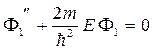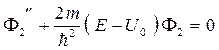, (1.6)

.

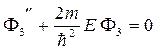Проведем предварительный анализ данной задачи, тех проблем, которые встретятся при ее рассмотрении, и составим план ее решения. На таком предварительном этапе также возможно использование аналитического пакета, например, Maple. Для этого попытаемся получить общие решения дифференциальных уравнений (1.6). Однако необходимо конкретизировать знак величины E, а также знак разности 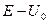. Ясно, что E, будучи энергией частицы, не может быть отрицательной. Что касается разности, то она может быть и отрицательной, и положительной, в зависимости от того, меньше или больше величина E высоты потенциального барьера (1.5), изображенного на рисунке 1.4. Предположим для определенности, что 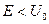. Кроме того, необходимо уточнить и положительный знак 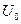(не следует забывать, что если для нас что-либо и очевидно, то программа этого знать не может!). Отразим все это в операторе assume, который описывает свойства переменных и соотношения между ними. Опишем после этого уравнения (1.6), придав им имена, например, eq1, eq2, eq3, и воспользуемся оператором dsolve (без каких-либо дополнительных опций) для получения общих решений этих уравнений. Последние будут выданы программой лишь в том случае, если они выражаются через элементарные или хотя бы специальные функции. Все вышеописанное реализуется в следующей программе.

> restart:

> assume(U0> 0, E> 0, E< U0):

> eq1: =diff(phi1(x), x$2)+(2*m/h^2)*E*phi1(x); eq2: =diff(phi2(x), x$2)+(2*m/h^2)*(E-U0)*phi2(x); eq3: =diff(phi3(x), x$2)+(2*m/h^2)*E*phi3(x);

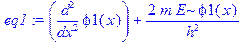
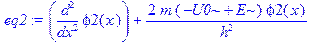
> dsolve(eq1); dsolve(eq2); dsolve(eq3);

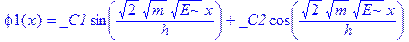
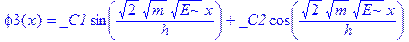
Отметим, что величины, описанные с помощью оператора assume, в дальнейшем отображаются в виде с тильдой: E~, U₀~.

Общие решения уравнений получены, и они выражаются через элементарные функции. Мы приходим к следующим выводам. Решения в областях 1 и 3 удобно выразить не через E, а через параметр

(1.7)

(сравните с [2, с. 84]). Эти решения представляют собой линейные комбинации с неопределенными коэффициентами функций и 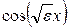. Но поскольку общее решение исходного уравнения (1.2) ищется в виде (1.3), т.е. в виде экспонент с мнимым показателем, будем считать их линейными комбинациями функци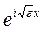й и 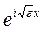(это возможно ввиду полной произвольности коэффициентов). Таким образом, в области 1 решение имеет вид

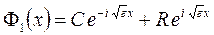, (1.8)

а в области 3 такой вид

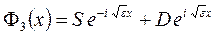. (1.8)

Вспоминая, что, согласно (1.3), для получения общей волновой функции Ψ эти стационарные функции надо умножить на 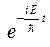. Таким образом получим:

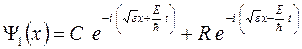
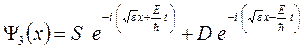(1.9)

Итак, функции Ψ ₁ и Ψ ₂ представляют собой суперпозиции волн, распространяющихся в отрицательном направлении оси OX (с амплитудами С и S) и в положительном направлении (с амплитудами R и D). Иными словами, имеются волны (частицы), приходящие «из бесконечности» слева и справа, которые частично отражаются от барьера, частично проходят (туннелируют) сквозь него, и такие отраженные и преломленные волны накладываются на исходные. Вычислить коэффициент прохождения через барьер в такой ситуации затруднительно. Необходимо «очистить» картину, а именно: пусть имеется поток частиц, приходящих из бесконечности, например, справа, причем амплитуда этого потока нормирована на единицу. Слева от барьера тогда будет распространяться преломленная волна слева направо (с амплитудой S), а справа от него, помимо падающей, будет также отраженная волна с амплитудой R (как изображено с помощью стрелок на рисунке 1.4). Таким образом, в формулах (1.7) – (1.9) должно быть 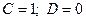, т.е. функции (1.7), (1.8) должны иметь вид

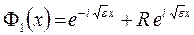
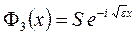(1.10)

В этом случае квадраты амплитуд 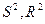будут представлять собой коэффициенты прохождения и отражения соответственно, причем должен выполняться закон сохранения числа частиц

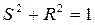. (1.11)

Соотношение (1.11) должно получиться автоматически и будет являться одним из критериев правильности проделанных вычислений.

Добиться выполнения выражений (1.10) можно, наложив некоторые дополнительные краевые условия, например, такие:

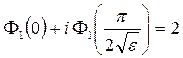
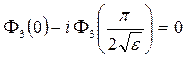. (1.12)

Помимо этого, должны удовлетворяться граничные условия непрерывности функций и их первых производных на границах областей 1, 2 и 3, т.е. в точках :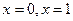

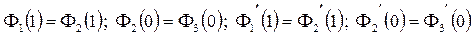(1.13)

Итого имеется три уравнения второго порядка (1.6), в решения которых входят шесть произвольных констант. С другой стороны, имеются два краевых условия (1.12) и четыре краевых условий (1.13) – итого шесть условий. Следовательно, решение не будет содержать произвольных констант, т.е. будет полностью определенным. В частности, как указывалось выше, соотношение (1.11) должно будет выполняться безусловно, так как у нас не остается свободных констант для его удовлетворения.

На данном этапе анализа задачи, после выполнения предварительных пробных расчетов (в нашем случае это общие решения дифференциальных уравнений) и сделанных из них выводов, надо сформулировать план решения задачи и определить, что именно мы ожидаем от применения аналитических пакетов. В данном случае необходимо сделать следующее:

а) решить систему уравнений (1.6) с краевыми условиями (1.12), (1.13);

б) из полученных функций 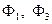выделить выражения для S, R и возвести в квадрат их модули – это и будут коэффициенты прохождения и отражения от барьера;

в) проверить правильность вычислений, посчитав сумму квадратов коэффициентов S, R, которая, согласно (1.11), должна равняться единице;

г) проанализировать полученное выражение для коэффициента прохождения, в первую очередь физический интерес представляет исследование его зависимости от энергии частицы E, сравнить с известными выражениями (задача учебная!);

д) для полноты картины построить график волновых функций во всей области, проверить «сшивание» функций и их первых производных, проанализировать поведение волновой функции внутри барьера.

На каких же этапах будет полезно и/или необходимо применение аналитического пакета? В пункте а), в принципе, можно обойтись и без него, проведя «ручные» вычисления, поскольку общие решения содержат только элементарные функции. Вспомнив, однако, что функций у нас три, каждая из которых содержит по две произвольные константы, а краевых условий шесть, становится ясно, что вычисления предстоят весьма громоздкие, а чем более они громоздки, тем больше вероятность ошибиться. И это для такой простейшей задачи, как одномерный и прямоугольный потенциальный барьер! Она, конечно, может быть решена вручную, что и было сделано задолго до появления аналитических пакетов и вообще компьютеров. Интересно тем не менее, что даже в таком фундаментальном курсе квантовой механики, как [2], детальный вывод коэффициента прохождения не приводится, автор пишет [2, с.101]: «Ограничимся тем, что дадим результат вычисления коэффициента прохождения:

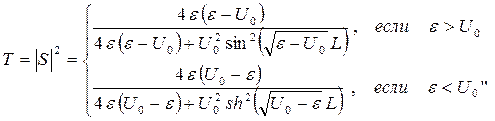(1.14)

(здесь L – длина барьера, в нашем случае 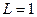). То есть вычисления возможны, но настолько громоздки и «рутинны», что А. Мессиа не посчитал целесообразным включение их в изложение своего курса. А немного более сложные (и реалистичные) задачи практически уже не позволяют проведения ручных вычислений. Наш учебный пример приобретает, таким образом, большое значение как некая базовая задача, на которой необходимо «обкатать» технологию применения аналитических пакетов и который можно будет впоследствии обобщать на более сложные и интересные случаи.

В пунктах б), в) также возможно в принципе обойтись без компьютера, но ввиду громоздкости, аналитический пакет позволит провести вычисления проще и быстрее. Что же касается графиков, то преимущества применения компьютеров для их построения и анализа совершенно очевидны.

Итак, в случае нашей задачи применение «компьютерной алгебры» позволяет произвести вычисления с неизмеримо меньшими затратами труда и времени, чем «вручную» и является практически необходимым. Причем вычисления будут проводиться точно, т.е. будет задействована аналитическая компонента пакета, без использования его численной части.

Начало программы практически идентично приведенной выше программе для предварительного анализа: описание знаков E и 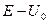, задание уравнений. Отличие состоит в том, что теперь необходимо задать также граничные условия (1.12), (1.13), причем удобно всю совокупность этих условий обозначить каким-либо именем, например ics. Также имеет смысл дать некоторое имя системе дифференциальных уравнений, например ode. Кроме того, зададим для определенности значения массы и постоянной Планка: 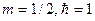и высоты барьера 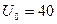(для сопоставления с графиком, приведенном в [2, с.102], который соответствует такому значению). Опишем также параметр ε (1.7).

> restart:

> U0: =40: m: =1/2: h: =1:

> assume(E> 0, E< U0):

> epsilon: =(2*m/h^2)*E;

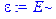
> eq1: =diff(phi1(x), x$2)+(2*m/h^2)*E*phi1(x); eq2: =diff(phi2(x), x$2)+(2*m/h^2)*(E-U0)*phi2(x); eq3: =diff(phi3(x), x$2)+(2*m/h^2)*E*phi3(x);

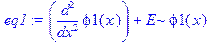
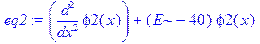
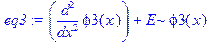
> ode: =eq1, eq2, eq3:

> ics: = phi1(1)=phi2(1), phi2(0)=phi3(0),

D(phi1)(1)=D(phi2)(1), D(phi2)(0)=D(phi3)(0), phi1(0)+I*phi1(Pi/2/sqrt(epsilon))=2, phi3(0)-I*phi3(Pi/2/sqrt(epsilon))=0;

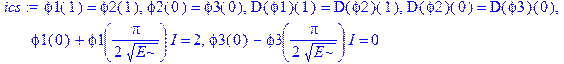
Применим теперь ключевой оператор нашей программы dsolve, производящий точное решение дифференциальных уравнений, но в отличие от его применения на предварительном этапе без каких-либо опций (тогда в результате получили общие решения с неопределенными коэффициентами), теперь этот оператор будет использован в режиме нахождения решений с граничными условиями. Совершенно необходимо дать решению какое-либо имя, например R, если мы хотим далее использовать это решение, а не просто посмотреть на его распечатку. Кстати говоря, такая распечатка не является необходимой, и можно было бы поставить в конце оператора двоеточие, чтобы избежать отображения громоздкого выражения на экране. Однако из методических соображений, поставим в конце точку с запятой и выведем решение на экран, поскольку на практике всегда именно так и приходится делать с тем, чтобы убедиться, что оно действительно получено и посмотреть на него, что называется «вживую». Далее можно вернуть курсор на строчку оператора, поменять точку с запятой на двоеточие и выполнить оператор еще раз, в результате распечатка исчезнет. Кроме того, распечатка решения служит иллюстрацией к вышеприведенным рассуждениям о громоздкости задачи и преимуществах применения компьютерной алгебры перед ручными вычислениями.

> R: =dsolve({ode, ics});

.

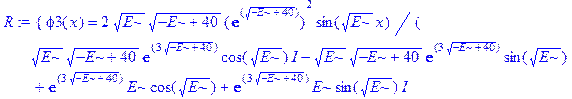
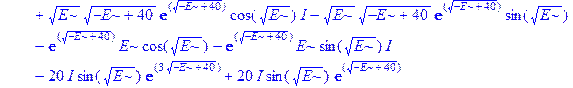
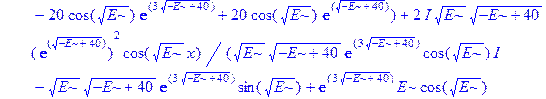
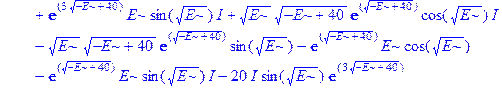
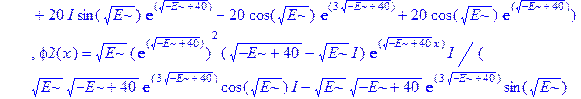
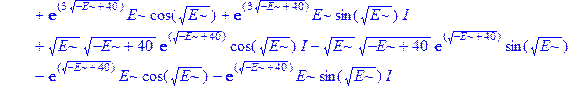
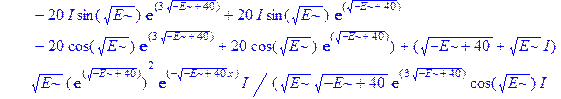
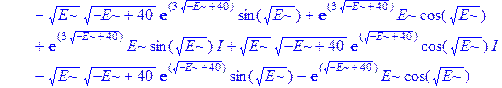
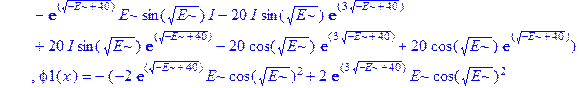
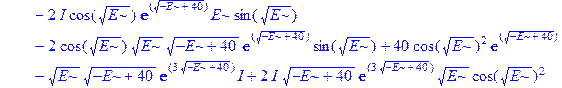
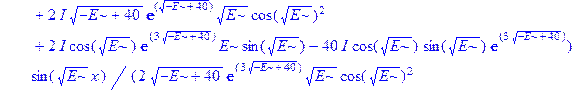
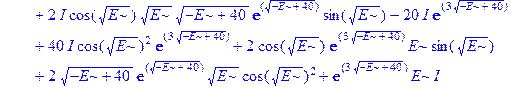
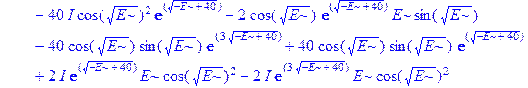
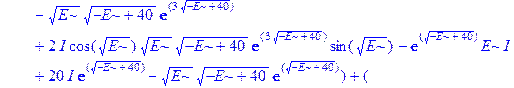
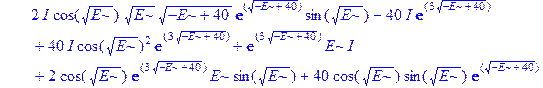
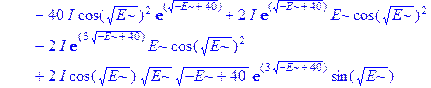
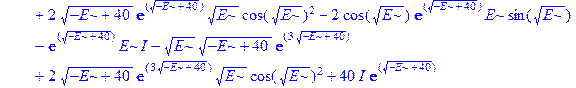
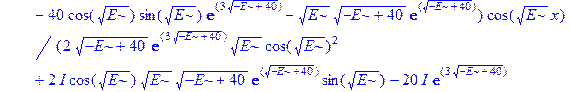
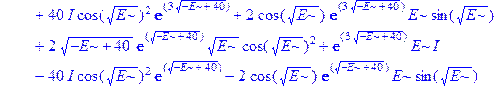
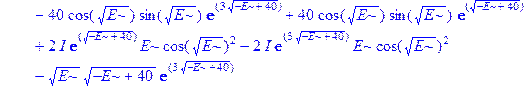
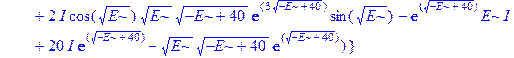Получившееся выражение имеет структуру 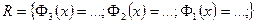. Далее можно применить оператор присваивания assign к имени, под которым у нас фигурирует решение – R. В результате произойдет присваивание всем величинам, входящим в R, их значений, фигурирующих в этом массиве. Т.е. 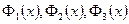обретут свои выражения согласно распечатанному массиву R. А тогда, имея в виду (1.10), можно получить амплитуду прошедшей сквозь барьер волны S, просто подстави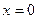в в 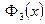, используя уже знакомый нам оператор subs. Далее вычисляем коэффициент прохождения как квадрат модуля S, умножая S на его комплексно сопряженное (оператор conjugate).

> assign(R):

> S: =simplify(subs(x=0, phi3(x)));

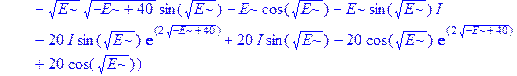
> > T: =simplify(S*conjugate(S));

.

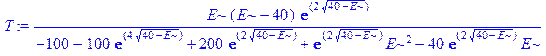Обратим внимание на оператор simplify, который очень часто употребляется в Maple. Как следует из его названия, он позволяет упрощать выражения, что бывает необходимо не только из эстетических соображений, но и для возможности продолжения вычислений, которые иначе, выражаясь компьютерным языком, «затыкаются». Читателю рекомендуется, например, выполнить последний оператор без применения simplify и сравнить полученные выражения.

Итак, коэффициент прохождения T получен. Аналогично можно получить коэффициент отражения как квадрат модуля амплитуды R, которую, согласно (1.10), можно извлечь из 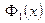следующим образом:

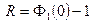. (1.15)

Однако мы не можем использовать в программе имя R, которое уже занято. Обозначим поэтому амплитуду отраженной волны малой буквой r, а квадрат ее модуля как r2:

> r: =simplify(subs(x=0, phi1(x))-1): r2: =simplify(evalc(r*conjugate(r)));

.

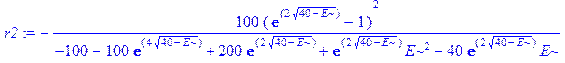Теперь все готово для проверки соотношения (1.11):

> simplify(r2+T);

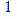
(попробуйте опять выполнить этот оператор без simplify, в виде r2+T и сравните результаты!)

Сравним полученный коэффициент прохождения T с известным из литературы выражением (1.14). Опишем формулу (1.14) для случая 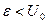под именем Q. Равны ли между собой Q и T? Применим simplify к их разности:

> Q: =4*epsilon*(U0-epsilon)/(4*epsilon*(U0-epsilon)+U0^2*sinh(sqrt(U0-epsilon))^2);

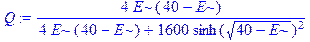
> simplify(T-Q);

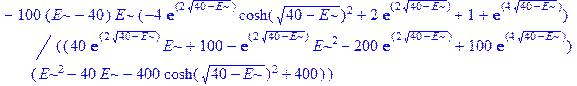
Ожидаемого нуля для T – Q не получилось. Тем не менее, поскольку мы надеемся, что вычисления проведены правильно, выражения T и Q должны совпадать! Подставим в T и Q вместо E одно и то же значение E< U₀:

> evalf(subs(E=38, T)); evalf(subs(E=38, Q));

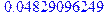
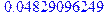
Значения совпадают. Более того, анализируя структуру выражений, можно заметить, что они зависят от разности U₀ (в нашем примере 40) и E, которая стоит под корнем. При вычислениях мы предполагали E< U₀. Можно предположить, что при E> U₀, поскольку разность E – U₀ сменит знак, появится мнимая единица и экспоненты в нашем выражении для T дадут тригонометрические функции, и наше вычисленное T перейдет в выражение (1.14) для случая E> U₀. Действительно, легко видеть, что в (1.14) оба случая представляют собой практически одно и то же выражение, которые переходят одно в другое при смене знака E – U₀. Проверим, подставив в T и Q вместо E одно и то же значение E> U₀:

> evalf(subs(E=50, T)); evalf(subs(E=50, Q));

.

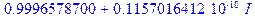
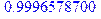Выражения, как и следовало ожидать, совпали. Отметим, что небольшой «дефект» в первом выражении, возникший из-за применения численных расчетов в функции evalf, никакого значения не имеет, поскольку равен 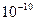, т.е. нулю. Наберемся теперь смелости и построим зависимости T и Q от E на одном графике в диапазоне от 0 до 4U₀. Оператор построения графиков plot имеет много опций, которые можно посмотреть в Help, набрав в командной строке знак вопроса и то слово, которым вы интересуетесь:

>? plot

Мы используем лишь небольшое число из возможностей оператора построения графиков. Поскольку строятся две кривые на одном графике, их имена необходимо поместить в массив с помощью фигурных скобок. Далее надо указать переменную, откладываемую по горизонтальной оси и диапазон ее изменения (отметьте, что применяются две, а не три точки!) Поскольку мы ожидаем, что обе кривые совпадут, имеет смысл построить их по-разному, например, одну в виде сплошной, а другую в виде точечной линии. Это можно сделать, используя опцию style, перечисление параметров в которой соответствует порядку перечисления выражений в фигурных скобках. Наконец, с помощью опции title напишем название графика.алее надо указать переменную, откладываемую по горизонтальной оси и диапазон ее изменения (о же выражение

> plot({T, Q}, E=0..4*U0, style=[line, point], title=" Коэффициент прохождения в зависимости от энергии");

График показан на рисунке 1.5. Полученный график в точности совпадает с [2, c. 102]. Таким образом, нам удалось получить нетривиальный результат, приведенный в [2] без вывода и доказательства. Это сделано с минимальными затратами труда и времени лишь благодаря применению численно-аналитического пакета компьютерной алгебры.

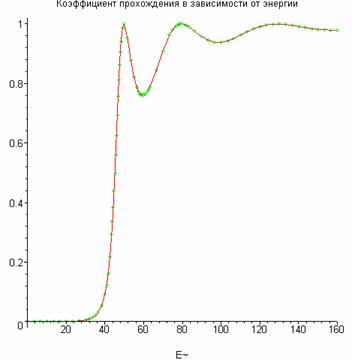
Рис. 1.5. Изменение коэффициента прохождения в зависимости от энергии для потенциального барьера, показанного на рисунке 1.4. Принято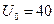

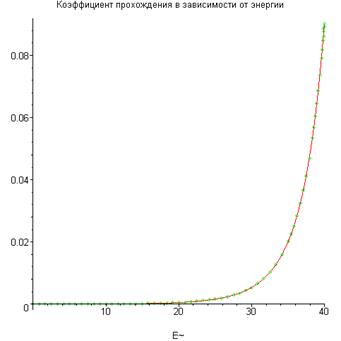
Рис. 1.6. Изменение коэффициента прохождения в зависимости от энергии для потенциального барьера на рисунке 1.4, в диапазоне 0 < E < U _о. Принято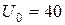

Можно более подробно просмотреть график в диапазоне E< U₀:

> plot({T, Q}, E=0..U0, style=[line, point], title=" Коэффициент прохождения в зависимости от энергии");

Графики T и Q совпадают. Теперь нет никакого сомнения: полученное нами выражение для коэффициента прохождения совпадает с известным из литературы выражением (1.14), причем для частиц с энергиями как меньшими, так и большими высоты барьера. Но почему же не удалось упростить выражения так, чтобы разность T – Q обратилась в ноль? Оператор simplify сам по себе не справился с этой задачей, что нередко случается в Maple. Иногда такие трудности удается обойти с помощью дополнительных опций в simplify (посмотрите в Help), иногда имеет смысл комбинировать simplify с такими операторами, как evalc (от слов evaluate complex –явное выделение действительной и мнимой части из комплексного выражения), evalf, expand, coeff и т.п. (ознакомьтесь с этими операторами в Help). Читателю предоставляется возможность попытаться добиться обращения разности T – Q в ноль, комбинируя опции и операторы. Здесь добьемся этого по-другому: «поможем» оператору simplify, заменив в выражении для Q гиперболический синус (sinh) на его явное выражение через экспоненты :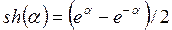

> Q: =4*epsilon*(U0-epsilon)/(4*epsilon*(U0-epsilon)+U0^2*((exp(sqrt(U0-epsilon))-exp(-sqrt(U0-epsilon)))/2)^2);

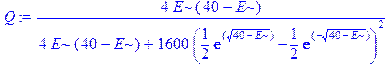
> simplify(T-Q);

.

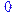Наконец, построим графики получившихся (стационарных) волновых функций (1.10) (точнее, квадратов их модулей). Воспользуемся операторами evalf, evalc, simplify для приведения выражений к максимально упрощенному виду и для вычисления всех входящих в них коэффициентов. Подставим 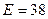, т.е. значение немного ниже высоты барьера.

> EE: =38:

> f3: =simplify(evalf(evalc(subs(E=EE, phi3(x))*conjugate(subs(E=EE, phi3(x)))))); f1: =simplify(evalf(evalc(subs(E=EE, phi1(x))*conjugate(subs(E=EE, phi1(x)))))); f2: =simplify(evalf(evalc(subs(E=EE, phi2(x))*conjugate(subs(E=EE, phi2(x))))));

.

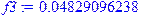
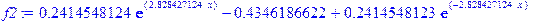Как и следовало ожидать, решение внутри барьера выражается через экспоненты, а вне барьера – через тригонометрические функции. Естественно, в области слева от барьера после всех упрощений получилась константа. Напомним, что это не сама волновая функция, а квадрат ее модуля, т.е. плотность вероятности, а из (1.10) ясно, что квадрат модуля функции 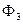равен S², т.е. коэффициенту прохождения, значение которого при 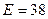мы уже получали выше. Построим графики этих функций, причем здесь в отличие от предыдущего применения оператора plot имеем не только несколько функций, но и у каждой свой интервал изменения переменной. Как построить такой график – ясно из следующей строчки.

> plot({[x, f1, x=1..3], [x, f2, x=0..1], [x, f3, x=-1..0]});

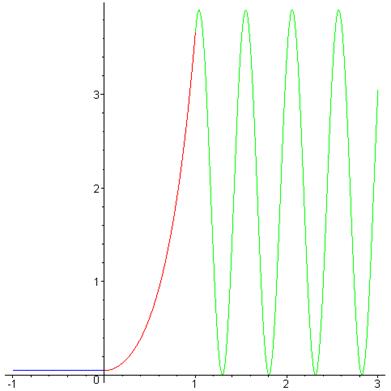
Рис. 1.7. Плотность вероятности для частицы с энергией при высоте барьера 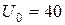. Барьер локализован на участке от 0 до 1

Список литературы к теме 1

Использованная литература:

1. Сдвижков О.А. Математика на компьютере: Maple 8. – Солон-пресс, 2003.- 244 с.

2. Мессиа Альберт. Квантовая механика. – М.: Наука, 1978. – 480 с.

3. Дьяконов В.П. Maple 9.5/10 в математике, физике и образовании. Серия «Библиотека профессионала.– М.: Изд-во «Солон», 2006. – 720 с.

Рекомендуемая литература:

1. Васильев А.Н. Maple 8. Самоучитель. – М.: Диалектика, Вильямс, 2003.

2. Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple 9. – М.: Изд-во «НТ Пресс», 2006. – 496 с.

3. Гандер В., Гржебичек И. Решение задач в научных вычислениях с применением Maple и MATLAB. – М.: Изд-во «Вассамедина», 2005. – 520 с.